2018-2019学年初中数学华师大版七年级下册10.3.2 旋转的特征 同步练习
试卷更新日期:2019-02-25 类型:同步测试
一、选择题
-
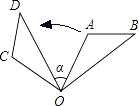
1. 如图,△OAB绕点O逆时针旋转85°得到△OCD,若∠A=110°,∠D=40°,则∠α的度数是( )
 A、35° B、45° C、55° D、65°2. 如图,将△ABC绕点A顺时针旋转 60°得到△AED,若线段AB=3,则BE=( )
A、35° B、45° C、55° D、65°2. 如图,将△ABC绕点A顺时针旋转 60°得到△AED,若线段AB=3,则BE=( )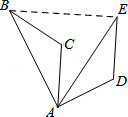 A、2 B、3 C、4 D、53. 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
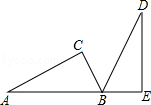
A、2 B、3 C、4 D、53. 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )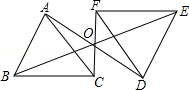 A、点A与点D是对应点 B、BO=EO C、∠ACB=∠FDE D、AB∥DE4. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则BE的长为( )
A、点A与点D是对应点 B、BO=EO C、∠ACB=∠FDE D、AB∥DE4. 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则BE的长为( )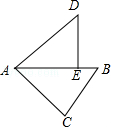 A、1 B、2 C、3 D、45. 如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连接CE,DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
A、1 B、2 C、3 D、45. 如图,E,F分别是正方形ABCD的边AB,BC上的点,BE=CF,连接CE,DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )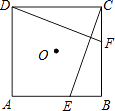 A、45° B、60° C、90° D、120°6.
A、45° B、60° C、90° D、120°6.如图,将Rt△ABC(∠B=25°)绕点A顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
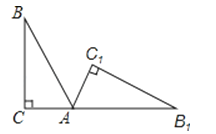 A、65° B、80° C、105° D、115°7. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )
A、65° B、80° C、105° D、115°7. 如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的大小是( )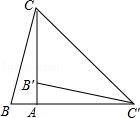 A、32° B、64° C、77° D、87°
A、32° B、64° C、77° D、87°二、填空题
-
8.
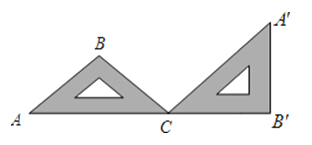
如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A,C,B′三点共线,那么旋转角度的大小为
 9. 如图,在△ABC中,∠BAC=60°,将△ABC绕着点A顺时针旋转40°后得到△ADE,则∠BAE= .
9. 如图,在△ABC中,∠BAC=60°,将△ABC绕着点A顺时针旋转40°后得到△ADE,则∠BAE= . 10.
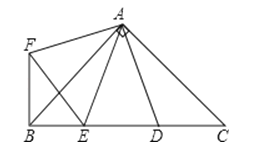
10.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连结EF.则∠EAF=
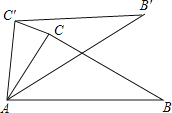
 11. 如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于度.
11. 如图,在梯形ABCD中,AD∥BC,将这个梯形绕点D按顺时针方向旋转,使点C落在边AD上的点C′处,点B落在点B′处,如果直线B′C′经过点C,那么旋转角等于度.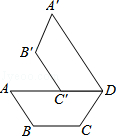 12. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= .
12. 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′= .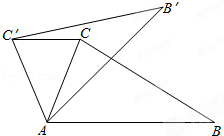
三、解答题
-
13. 如图,将△ABC绕点C顺时针方向旋转40°得△A′B′C′,若AC⊥A′B′,求∠BAC的度数.
 14.
14.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB , 求∠BAB′的度数.
 15.
15.如图,△ABC中,∠ACB=90°,AC=BC , 点D在边AB上,连接CD , 将线段CD绕点C顺时针旋转90°至CE位置,连接AE . 求证:AE=BD .
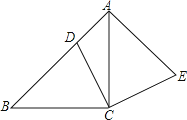 16. 在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
16. 在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图 (1)、指出旋转中心,并求出旋转角的度数.(2)、求出∠BAE的度数和AE的长.17. 已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)、指出旋转中心,并求出旋转角的度数.(2)、求出∠BAE的度数和AE的长.17. 已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.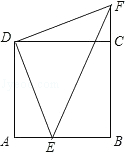 (1)、旋转中心是 . 旋转角为度.(2)、请你判断△DFE的形状,并说明理由.(3)、求四边形DEBF的周长和面积.
(1)、旋转中心是 . 旋转角为度.(2)、请你判断△DFE的形状,并说明理由.(3)、求四边形DEBF的周长和面积.