2018-2019学年初中数学华师大版七年级下册10.2 平移 同步练习
试卷更新日期：2019-02-25 类型：同步测试
一、选择题
-
1. 如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（ ）
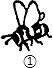A、
B、
C、
D、
2. 把图中的一个三角形先横向平移x格，再纵向平移y格，就能与另一个三角形拼合成一个四边形，那么x+y（ ）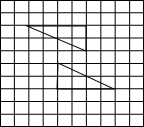
A、是一个确定的值 B、有两个不同的值 C、有三个不同的值 D、有三个以上不同的值3. 如图，线段AB=CD，AB与CD相交于O，且∠AOC=60°，CE是由AB平移所得，则AC+BD与AB的大小关系是（ ）
A、AC+BD＞AB B、AC+BD=AB C、AC+BD≥AB D、无法确定4. 某城市新建了一座游乐场，即日将完工．当施工者准备给游乐场用砖头砌上围墙时，发现在设计图纸中的某些数据已经模糊不清了（如图），从而无法计算出外围围墙的周长，因此无法备砖料．根据图中的标示，可计算出外围围墙的周长是（ ）
A、320米 B、260米 C、160米 D、100米5. 如图，将△ABE向右平移2cm得到△DCF，如果△ABE的周长是16cm，那么四边形ABFD的周长是（ ）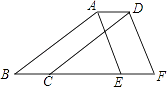
A、16cm B、18cm C、20cm D、21cm6. 如图，将边长为 的正方形ABCD沿对角线AC平移，使点A移至线段AC的中点A′处，得新正方形A′B′C′D′，新正方形与原正方形重叠部分（图中阴影部分）的面积是（ ）
A、 B、
C、1
D、
7. 如图，△ABC沿着BC方向平移得到△A′B′C′，点P是直线AA′上任意一点，若△ABC，△PB′C′的面积分别为S1 ， S2 ， 则下列关系正确的是（ ）
A、S1＞S2 B、S1＜S2 C、S1=S2 D、S1=2S28. 如图，△ABC的面积为12，将△ABC沿BC方向移到△A′B′C′的位置，使B′与C重合，连接AC′交A′C于D，则△C′DC的面积为（ ）
A、10 B、8 C、6 D、49.如图是一块长方形ABCD的场地，长AB=102m，宽AD=51m，从A、B两处入口的中路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪面积为（ ）
A、5050m2 B、5000m2 C、4900m2 D、4998m2二、填空题
-
10.
某景点拟在如图的矩形荷塘上架设小桥，若荷塘中小桥的总长为100米，则荷塘周长为 ．
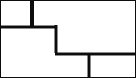11. 如图是一块从一个边长为50cm的正方形材料中剪出的垫片，现测得FG=5cm，则这个剪出的图形的周长是cm．
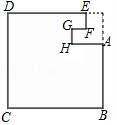12. 如图，在一块长方形ABCD草地上，AB=10，BC=15，有一条弯曲的柏油小路（小路任何地方的水平宽度都是2个单位），空白部分表示的草地面积是 ．
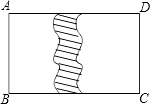13. 某宾馆在重新装修后，准备在大厅的主楼梯上铺上红色地毯，已知这种红色地毯的售价为每平方米32元，主楼道宽2米，其侧面与正面如图所示，则购买地毯至少需要元．
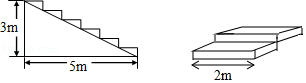14. 如图，∠1=70°，直线a平移后得到直线b，则∠2﹣∠3=°．
15. 如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到△DEF的位置，AB=10，DH=4，平移距离为6，则阴影部分的面积 ．
16.如图，立方体棱长为2cm，将线段AC平移到A1C1的位置上，平移的距离是cm.
三、解答题
-
17. 如图，宏达蔬菜基地内有一块长为216m，宽为108m的长方形土地，三条宽均为xm的田间小路把它分成面积相等的六块，分别种植西红柿、黄瓜、辣椒、芸豆、韭菜、茄子．
(1)、求每块种植蔬菜的长方形的面积．（用含x的多项式表示）(2)、当x=1.6m时，求每块种植蔬菜的长方形的面积．（精确到0.01m2）18.如图所示，有一条宽相等的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，若要硬化这条小路，且每平方米造价50元，则需要多少元钱？
19. 如图
(1)、图①是将线段AB向右平移1个单位长度，图②是将线段AB折一下再向右平移1个单位长度，请在图③中画出一条有两个折点的折线向右平移1个单位长度的图形．(2)、若长方形的长为a，宽为b，请分别写出三个图形中除去阴影部分后剩余部分的面积．(3)、如图④，在宽为10m，长为40m的长方形菜地上有一条弯曲的小路，小路宽为1m，求这块菜地的面积．20.将△ABC沿BC的方向平移得到△DEF．
(1)、若∠B=74°，∠F=26°，求∠A的度数；(2)、若BC=4.5cm，EC=3.5cm，求△ABC平移的距离．21. 如图已知直线CB∥OA，∠C=∠OAB=100°，点E、点F在线段BC上，满足∠FOB=∠AOB=α，OE平分∠COF．
(1)、用含有α的代数式表示∠COE的度数；(2)、若沿水平方向向右平行移动AB，则∠OBC：∠OFC的值是否发生变化？若变化找出变化规律；若不变，求其比值．22. 如图，已知MN∥PQ，B在MN上，C在PQ上，A在B的左侧，D在C的右侧，DE平分∠ADC，BE平分∠ABC，直线DE，BE交于点E，∠CBN=120°．
(1)、若∠ADQ=110°，求∠BED的度数；(2)、将线段AD沿DC方向平移，使得点D在点C的左侧，其他条件不变，若∠ADQ=n°，求∠BED的度数（用含n的代数式表示）