备考2019年高考数学一轮专题:第26讲 数系的扩充与复数的引入
试卷更新日期:2019-02-24 类型:一轮复习
一、选择题
-
1. i为虚数单位, ( )A、i B、
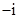 C、1
D、
C、1
D、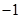 2. 若复数 ,则复数z在复平面内对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若复数 满足 ,则 的虚部为( )A、
2. 若复数 ,则复数z在复平面内对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若复数 满足 ,则 的虚部为( )A、 B、
B、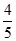 C、
C、 D、
D、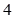 4. 已知复数 满足 ,则 ( )A、 B、 C、1 D、55. 已知复数 满足 ( 为虚数单位),则复数 的模为( )A、2 B、
4. 已知复数 满足 ,则 ( )A、 B、 C、1 D、55. 已知复数 满足 ( 为虚数单位),则复数 的模为( )A、2 B、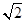 C、5
D、
6. 已知 其中 为虚数单位,则 ( )A、-1 B、1 C、2 D、37. 若复数(1–i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )A、(–∞,1) B、(–∞,–1) C、(1,+∞) D、(–1,+∞)8. 若复数 是实数(i为虚数单位),则实数 的值是( )A、1 B、2 C、3 D、49. 复数 (i为虚数单位)的共轭复数是( )
C、5
D、
6. 已知 其中 为虚数单位,则 ( )A、-1 B、1 C、2 D、37. 若复数(1–i)(a+i)在复平面内对应的点在第二象限,则实数a的取值范围是( )A、(–∞,1) B、(–∞,–1) C、(1,+∞) D、(–1,+∞)8. 若复数 是实数(i为虚数单位),则实数 的值是( )A、1 B、2 C、3 D、49. 复数 (i为虚数单位)的共轭复数是( )
A、1+i B、1−i C、−1+i D、−1−i10. ( )A、 B、 C、 D、11. 若 , ,则 ( )A、 B、 C、 D、二、填空题
-
12. 若复数 ( , 是虚数单位)是纯虚数,则a= .13. 已知i为虚数单位,若复数z满足 ,则复数z= .14. i是虚数单位,复数
15. 已知 是虚数单位,复数 满足 ,则 .16. 若复数 ,其中 是虚数单位,则 .17. 若复数z满足 |z-i|≤ (i为虚数单位), 则z在复平面内所对应的图形的面积为 .
18. 若 ,其中 都是实数, 是虚数单位,则 .三、解答题