备考2019年高考数学一轮专题:第25讲 平面向量的数量积
试卷更新日期:2019-02-24 类型:一轮复习
一、选择题
-
1. 已知向量 与 的夹角为120°, 则
 ( ) A、5 B、4 C、3 D、12. 如图,在圆 中,若 , ,则 的值等于( )
( ) A、5 B、4 C、3 D、12. 如图,在圆 中,若 , ,则 的值等于( ) A、
A、 B、
B、 C、
C、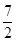 D、
3. 已知平面向量 , 的夹角为 ,且 , ,则 ( )A、1 B、2 C、
D、
3. 已知平面向量 , 的夹角为 ,且 , ,则 ( )A、1 B、2 C、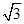 D、3
4. 设向量 , ,向量 与 的夹角为锐角,则 的范围为( )A、
D、3
4. 设向量 , ,向量 与 的夹角为锐角,则 的范围为( )A、 B、
B、 C、
C、 D、
D、 5. 已知平面向量 满足 ,且 ,则向量 的夹角 为( )A、 B、 C、 D、
5. 已知平面向量 满足 ,且 ,则向量 的夹角 为( )A、 B、 C、 D、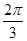 6. 已知a , b , e是平面向量,e是单位向量.若非零向量a与e的夹角为 ,向量b满足b2−4e·b+3=0,则|a−b|的最小值是( )
6. 已知a , b , e是平面向量,e是单位向量.若非零向量a与e的夹角为 ,向量b满足b2−4e·b+3=0,则|a−b|的最小值是( )
A、 −1 B、 +1 C、2 D、2−7. 下列说法正确的是( )A、若 与 共线,则 或者 B、若 ,则 C、若 中,点 满足 ,则点 为 中点 D、若 , 为单位向量,则8. 若向量 , ,满足 ,则实数 ( )A、 B、 C、 D、9. 平面向量 与 的夹角为 , , ,则 ( )A、 B、 C、3 D、710. 在边长为2的菱形 中, 则 在 方向上的投影为( )A、 B、 C、1 D、211. 如图,在四边形 中,已知 , ,则 的最小值为( ) A、1 B、2 C、3 D、412. 已知向量 , ,若 ,则实数 ( )A、 或 B、 或 C、 D、
A、1 B、2 C、3 D、412. 已知向量 , ,若 ,则实数 ( )A、 或 B、 或 C、 D、二、填空题
-
13. 等边△ABC中,边长为2,则 =14. 在平面直角坐标系 中,A为直线 上在第一象限内的点, ,以AB为直径的圆C(C为圆心)与直线l交于另一点D.若 ,则点A的坐标为15. 若 是夹角为 的两个单位向量, ,则 的夹角为 .16. 在△ABC中,CA=2CB=2, ,O是△ABC的外心, 若 =x +y ,则x+y= .17. 已知两不共线的非零向量 满足 , ,则向量 与 夹角的最大值是.18. 已知平面向量 的夹角为 , ,则 .
三、解答题
-
19. 设两个向量 ,满足 .(1)、若 ,求 的夹角.(2)、若 夹角为 ,向量 与 的夹角为钝角,求实数 的取值范围.20. 已知向量 = (1,2sinθ), = (sin(θ+ ),1),θ R。(1)、若 ⊥ ,求 tanθ的值;(2)、若 ∥ ,且 θ (0, ),求 θ的值