备考2019年高考数学一轮专题:第23讲 平面向量的概念及线性运算
试卷更新日期:2019-02-24 类型:一轮复习
一、选择题
-
1. 已知向量 , 满足 , ,则 的最小值是( )A、1 B、2 C、3 D、42. 如图所示,矩形 的对角线相交于点 , 为 的中点,若 ( 、 为实数),则 ( )
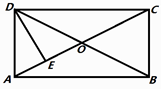 A、 B、 C、 D、3. 如果向量 =(k,1)与 =(6,k+1)共线且方向相反,那么k的值为( )A、-3 B、2 C、-
A、 B、 C、 D、3. 如果向量 =(k,1)与 =(6,k+1)共线且方向相反,那么k的值为( )A、-3 B、2 C、- D、
D、 4. 在△ABC中, ,且 ,则 =( )A、
4. 在△ABC中, ,且 ,则 =( )A、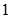 B、
B、 C、
C、 D、
D、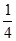 5. 设 是不共线的两个向量,已知 , ,则( )A、 三点共线 B、 三点共线 C、 三点共线 D、 三点共线6. 已知 ,下列向量中,与 反向的单位向量是( )
5. 设 是不共线的两个向量,已知 , ,则( )A、 三点共线 B、 三点共线 C、 三点共线 D、 三点共线6. 已知 ,下列向量中,与 反向的单位向量是( )
A、 B、 C、 D、7. 下列各组向量中,可以作为基底的是( )A、 , B、 , C、 , D、 ,8. 下列说法中:⑴若 是单位向量, 也是单位向量,则 与 的方向相同或相反;
⑵若向量 是单位向量,则向量 也是单位向量;
⑶两个相等的向量,若起点相同,则终点必相同.
正确的个数为( )
A、 B、 C、 D、9. 在 中,若 ,则 面积的最大值为( )A、 B、 C、 D、10. 已知正方形 的边长为 , , ,则 等于( )A、 B、 C、 D、二、填空题
-
11. 设向量 , 满足 , ,则 .12. 已知向量 ,若 且方向相反,则 .13. 与向量 反向的单位向量 =。14. 如图,在梯形ABCD中, ,P为线段CD上一点,且 ,E为BC的中点,若 ,则 的值为 .
 15. 已知正方形 的边长为2,则 .16. 若向量 , 满足 , ,则 的最小值是 .17. 如图,四边形 是边长为 的正方形,把各边三等分后,共有 个交点,从中选取两个交点作为向量,则与 平行且长度为 的向量有个.
15. 已知正方形 的边长为2,则 .16. 若向量 , 满足 , ,则 的最小值是 .17. 如图,四边形 是边长为 的正方形,把各边三等分后,共有 个交点,从中选取两个交点作为向量,则与 平行且长度为 的向量有个.
三、解答题
-
18. 已知 , , 分别为 三个内角 的对边, , .(1)、求 ;(2)、若 的中点, ,求 , .19. 已知 , , 是不共线的三点,且 .(1)、若 ,求证: , , 三点共线;(2)、若 , , 三点共线,求证: .20. 已知 是互相垂直的两个单位向量,
(Ⅰ)求 的值;
(Ⅱ)当 为何值时, 与 共线.