2017年黑龙江省双鸭山市宝清县高考数学一模试卷（理科）

试卷更新日期：2017-04-19 类型：高考模拟

进入出卷网下载

一、选择题

1. 若M={x|﹣2≤x≤2}，N={x|y=log₂（x﹣1）}，则M∩N=（）

A、{x|﹣2≤x＜0} B、{x|﹣1＜x＜0} C、{﹣2，0} D、{x|1＜x≤2}

查看试题解析
2. 复数z满足z（1+i）=|1﹣i|，则复数z的虚部是（）

A、﹣1 B、1 C、﹣ $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 已知向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{2 π}{3}$ ，| $\vec{a}$ |= $\sqrt{2}$ ，则 $\vec{a}$ 在 $\vec{b}$ 方向上的投影为（）

A、 $\frac{\sqrt{6}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、- $\frac{\sqrt{2}}{2}$ D、- $\frac{\sqrt{6}}{2}$

查看试题解析
4. 中国古代数学著作《算法统宗》中有这样一个问题：“三百七十八里关，初行健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还．”其大意为：“有一个人走了378里路，第一天健步行走，从第二天起因脚痛每天走的路程为前一天的一半，走了6天后到达目的地．”问此人第4天和第5天共走了（）

A、60里 B、48里 C、36里 D、24里

查看试题解析
5. 某三棱锥的三视图如图所示，则该三棱锥的表面积是（）

A、 $2 + \sqrt{5}$ B、 $4 + \sqrt{5}$ C、 $2 + 2 \sqrt{5}$ D、5

查看试题解析
6. 执行如图的程序框图，若程序运行中输出的一组数是（x，﹣12），则x的值为（　　）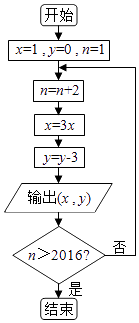

A、27 B、81 C、243 D、729

查看试题解析
7. 数列{a_n}是正项等比数列，{b_n}是等差数列，且a₆=b₇ ，则有（　　）

A、a₃+a₉≤b₄+b₁₀ B、a₃+a₉≥b₄+b₁₀ C、a₃+a₉≠b₄+b₁₀ D、a₃+a₉与b₄+b₁₀ 大小不确定

查看试题解析
8. 在第二届乌镇互联网大会中，为了提高安保的级别同时又为了方便接待，现将其中的五个参会国的人员安排酒店住宿，这五个参会国要在a、b、c三家酒店选择一家，且这三家至少有一个参会国入住，则这样的安排方法共有（）

A、96种 B、124种 C、130种 D、150种

查看试题解析
9. 已知实数x，y满足不等式组 ${\begin{matrix} x \geq 0 \\ x + y \leq 2 \\ y \geq x \end{matrix}$ ，若目标函数z=kx+y仅在点（1，1）处取得最小值，则实数k的取值范围是（）

A、（﹣1，+∞） B、（﹣∞，﹣1） C、（1，+∞） D、（﹣∞，1）

查看试题解析
10. 设a= $\int_{1}^{e^{2}}$ $\frac{1}{x}$ dx，则二项式（x²﹣ $\frac{a}{x}$ ）⁵的展开式中x的系数为（）

A、40 B、﹣40 C、80 D、﹣80

查看试题解析
11. 已知球O是的棱长为1的正方体ABCD﹣A₁B₁C₁D₁的内切球，则平面ACD₁截球O的截面面积为（）

A、π B、 $\frac{π}{2}$ C、 $\frac{π}{3}$ D、 $\frac{π}{6}$

查看试题解析
12. 设△A_nB_nC_n的三边长分别为a_n ， b_n ， c_n ， △A_nB_nC_n的面积为S_n ， n=1，2，3…若b₁＞c₁ ， b₁+c₁=2a₁ ， a_n₊₁=a_n ， $b_{n + 1} = \frac{c_{n} + a_{n}}{2}$ ， $c_{n + 1} = \frac{b_{n} + a_{n}}{2}$ ，则（）

A、{S_n}为递减数列 B、{S_n}为递增数列 C、{S_2n_﹣₁}为递增数列，{S_2n}为递减数列 D、{S_2n_﹣₁}为递减数列，{S_2n}为递增数列

查看试题解析

二、填空题.

13. 已知α∈（ $\frac{π}{2}$ ，π），且sin $\frac{α}{2}$ +cos $\frac{α}{2}$ = $\frac{\sqrt{6}}{2}$ ，则cosα的值．

查看试题解析
14. 已知函数f（x）= ${\begin{matrix} 2^{x} - 1 ， x > 0 \\ - x^{2} - 2 x ， x \leq 0 \end{matrix}$ ，若函数g（x）=f（x）﹣m有3个零点，则实数m的取值范围是．

查看试题解析
15. 设曲线y=xⁿ⁺¹（n∈N⁺）在点（1，1）处的切线与x轴的交点的横坐标为x_n ，则log₂₀₁₅x₁+log₂₀₁₅x₂+…+log₂₀₁₅x₂₀₁₄的值为．

查看试题解析
16. 函数f（x）=lnx+ax存在与直线2x﹣y=0平行的切线，则实数a的取值范围为

查看试题解析

三、解答题：解答写出文字说明、证明过程或演算过程．

17. 在锐角△ABC中， $\frac{b^{2} - a^{2} - c^{2}}{a c}$ = $\frac{\cos (A + C)}{\sin A \cos A}$

(1)、求角A；

(2)、若a= $\sqrt{2}$ ，求bc的取值范围．

查看试题解析
18. 2016年上半年，股票投资人袁先生同时投资了甲、乙两只股票，其中甲股票赚钱的概率为 $\frac{1}{3}$ ，赔钱的概率是 $\frac{2}{3}$ ；乙股票赚钱的概率为 $\frac{1}{4}$ ，赔钱的概率为 $\frac{3}{4}$ ．对于甲股票，若赚钱则会赚取5万元，若赔钱则损失4万元；对于乙股票，若赚钱则会赚取6万元，若赔钱则损失5万元．
（Ⅰ）求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率；
（Ⅱ）试求袁先生2016年上半年同事投资甲、乙两只股票的总收益的分布列和数学期望．

查看试题解析
19. 如图，斜三棱柱ABC﹣A₁B₁C₁的底面是直角三角形，∠ACB=90°，点B₁在底面内的射影恰好是BC的中点，且BC=CA=2．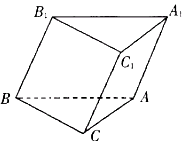

(1)、求证：平面ACC₁A₁⊥平面B₁C₁CB；

(2)、若二面角B﹣AB₁﹣C₁的余弦值为 $- \frac{5}{7}$ ，求斜三棱柱ABC﹣A₁B₁C₁的高．

查看试题解析
20. 如图，在平面直角坐标系xOy中，椭圆E： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的焦距为2，且过点（ $\sqrt{2}$ ， $\frac{\sqrt{6}}{2}$ ）．

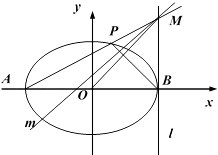(1)、求椭圆E的方程；

(2)、若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M．
①设直线OM的斜率为k₁ ，直线BP的斜率为k₂ ，求证：k₁k₂为定值；
②设过点M垂直于PB的直线为m．求证：直线m过定点，并求出定点的坐标．

查看试题解析
21. 已知函数f（x）=lnx﹣x．

(1)、求函数f（x）的单调区间；

(2)、若方程f（x）=m（m＜﹣2）有两个相异实根x₁ ， x₂ ，且x₁＜x₂ ，证明：x₁•x₂²＜2．

查看试题解析
22. [选修4-4：坐标系与参数方程选讲]
在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴，建立极坐标系，曲线C₁的参数方程为 ${\begin{matrix} x = 2 \sqrt{2} \cos α \\ y = 2 \sin α \end{matrix} (α \in R ， α$ 为参数），曲线C₂的极坐标方程为 $ρ \cos θ - \sqrt{2} ρ \sin θ - 5 = 0$ ．

(1)、求曲线C₁的普通方程和曲线C₂的直角坐标方程；

(2)、设P为曲线C₁上一点，Q曲线C₂上一点，求|PQ|的最小值．

查看试题解析
23. [选修4-5：不等式选讲]
已知函数f（x）=|x﹣a|+|2x﹣1|（a∈R）．
（Ⅰ）当a=1时，求f（x）≤2的解集；
（Ⅱ）若f（x）≤|2x+1|的解集包含集合[ $\frac{1}{2}$ ，1]，求实数a的取值范围．

查看试题解析