2017年浙江省宁波市七校联考中考数学一模试卷
试卷更新日期:2017-04-19 类型:中考模拟
一、选择题
-
1. 下列计算正确的是( )A、 B、(a2)3=a5 C、2a﹣a=2 D、a•a3=a42. 2016年鄞州区财政收入仍保持持续增长态势,全年财政收入为373.9亿元,其中373.9亿元用科学记数法表示为( )A、373.9×108元 B、37.39×109元 C、3.739×1010元 D、0.3739×10113. 如图是由五个相同的小立方块搭成的几何体,则它的俯视图是( )
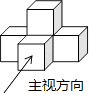 A、
A、 B、
B、 C、
C、 D、
D、 4. 使代数式 有意义的x的取值范围为( )A、x>2 B、x≠0 C、x<2 D、x≠25. 一组数据为1,5,3,4,5,6,这组数据的众数、中位数分为( )A、4,5 B、5,4.5 C、5,4 D、3,26.
4. 使代数式 有意义的x的取值范围为( )A、x>2 B、x≠0 C、x<2 D、x≠25. 一组数据为1,5,3,4,5,6,这组数据的众数、中位数分为( )A、4,5 B、5,4.5 C、5,4 D、3,26.如图,直线l1∥l2 , 以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67°,则∠1=( )
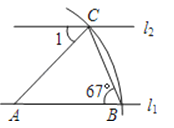 A、23° B、46° C、67° D、78°7. 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )
A、23° B、46° C、67° D、78°7. 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( ) A、π﹣2 B、 C、π﹣4 D、8. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )
A、π﹣2 B、 C、π﹣4 D、8. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( )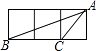 A、
A、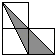 B、
B、 C、
C、 D、
D、 9.
9.如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(﹣1,0),顶点为(1,2),则结论:
①abc>0;②x=1时,函数最大值是2;③4a+2b+c>0;④2a+b=0;⑤2c<3b.
其中正确的结论有( )
 A、1个 B、2个 C、3个 D、4个10. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A﹣DME剪下围成一个圆锥,则圆锥的高为( )
A、1个 B、2个 C、3个 D、4个10. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A﹣DME剪下围成一个圆锥,则圆锥的高为( ) A、1 B、4 C、 D、11. 当m,n是实数且满足m﹣n=mn时,就称点Q(m, )为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y= 的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )A、1 B、 C、2 D、
A、1 B、4 C、 D、11. 当m,n是实数且满足m﹣n=mn时,就称点Q(m, )为“奇异点”,已知点A、点B是“奇异点”且都在反比例函数y= 的图象上,点O是平面直角坐标系原点,则△OAB的面积为( )A、1 B、 C、2 D、二、填空题
-
12. 分解因式:a2﹣4a+4= .13. 若方程x2+kx+9=0有两个相等的实数根,则k= .14. 直角三角形两直角边为3,4,则其外接圆和内切圆半径之和为 .15. 如图所示,一个宽为2cm的刻度尺在圆形光盘上移动,当刻度尺的一边与光盘相切时,另一边与光盘边缘两个交点处的读数恰好是“2”和“10”(单位:cm),那么该光盘的直径是 cm.
 16. 在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为6,△BCF的面积为9,△CEF的面积为6,则四边形ADFE的面积为 .
16. 在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为6,△BCF的面积为9,△CEF的面积为6,则四边形ADFE的面积为 . 17. 赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ x+ 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
17. 赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣ x+ 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为 .
三、解答题
-
18. 计算: ﹣|2 ﹣9tan30°|+( )﹣1﹣(1﹣π)0 .19. 宁波轨道交通4号线已开工建设,计划2020年通车试运营.为了了解镇民对4号线地铁票的定价意向,某镇某校数学兴趣小组开展了“你认为宁波4号地铁起步价定为多少合适”的问卷调查,并将调查结果整理后制成了如下统计图,根据图中所给出的信息解答下列问题:
 (1)、求本次调查中该兴趣小组随机调查的人数;(2)、请你把条形统计图补充完整;(3)、如果在该镇随机咨询一位居民,那么该居民支持“起步价为2元或3元”的概率是(4)、假设该镇有3万人,请估计该镇支持“起步价为3元”的居民大约有多少人?20. 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.
(1)、求本次调查中该兴趣小组随机调查的人数;(2)、请你把条形统计图补充完整;(3)、如果在该镇随机咨询一位居民,那么该居民支持“起步价为2元或3元”的概率是(4)、假设该镇有3万人,请估计该镇支持“起步价为3元”的居民大约有多少人?20. 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离. (1)、问BD与AB有什么数量关系,试说明理由;(2)、求信号发射点的深度.(结果精确到1m,参考数据: ≈1.414, ≈1.732)21. 如图,已知反比例函数y1= 与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.
(1)、问BD与AB有什么数量关系,试说明理由;(2)、求信号发射点的深度.(结果精确到1m,参考数据: ≈1.414, ≈1.732)21. 如图,已知反比例函数y1= 与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点. (1)、求k1 , k2 , b的值;(2)、求△AOB的面积;(3)、请直接写出不等式 x+b的解.22. 某服装店购进一批秋衣,价格为每件30元.物价部门规定其销售单价不高于每件60元,不低于每件30元.经市场调查发现:日销售量y(件)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.(1)、求出y与x的函数关系式,并写出自变量x的取值范围.(2)、求该服装店销售这批秋衣日获利w(元)与销售单价x(元)之间的函数关系式.(3)、当销售单价为多少元时,该服装店日获利最大?最大获利是多少元?23. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.
(1)、求k1 , k2 , b的值;(2)、求△AOB的面积;(3)、请直接写出不等式 x+b的解.22. 某服装店购进一批秋衣,价格为每件30元.物价部门规定其销售单价不高于每件60元,不低于每件30元.经市场调查发现:日销售量y(件)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.(1)、求出y与x的函数关系式,并写出自变量x的取值范围.(2)、求该服装店销售这批秋衣日获利w(元)与销售单价x(元)之间的函数关系式.(3)、当销售单价为多少元时,该服装店日获利最大?最大获利是多少元?23. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA. (1)、求证:BC=CD;(2)、分别延长AB,DC交于点P,若PB=OB,CD=2 ,求⊙O的半径.24. 若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.(1)、如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数;
(1)、求证:BC=CD;(2)、分别延长AB,DC交于点P,若PB=OB,CD=2 ,求⊙O的半径.24. 若一个四边形的一条对角线把四边形分成两个等腰三角形,且其中一个等腰三角形的底角是另一个等腰三角形底角的2倍,我们把这条对角线叫做这个四边形的黄金线,这个四边形叫做黄金四边形.(1)、如图1,在四边形ABCD中,AB=AD=DC,对角线AC,BD都是黄金线,且AB<AC,CD<BD,求四边形ABCD各个内角的度数; (2)、如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹);
(2)、如图2,点B是弧AC的中点,请在⊙O上找出所有的点D,使四边形ABCD的对角线AC是黄金线(要求:保留作图痕迹); (3)、在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.25.
(3)、在黄金四边形ABCD中,AB=BC=CD,∠BAC=30°,求∠BAD的度数.25.已知:如图一,抛物线y=ax2+bx+c与x轴正半轴交于A、B两点,与y轴交于点C,直线y=x﹣2经过A、C两点,且AB=2.
 (1)、求抛物线的解析式;(2)、
(1)、求抛物线的解析式;(2)、若直线DE平行于x轴并从C点开始以每秒1个单位的速度沿y轴正方向平移,且分别交y轴、线段BC于点E,D,同时动点P从点B出发,沿BO方向以每秒2个单位速度运动,(如图2);当点P运动到原点O时,直线DE与点P都停止运动,连DP,若点P运动时间为t秒;设s= ,当t为何值时,s有最小值,并求出最小值.
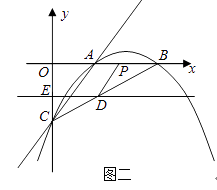 (3)、在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.
(3)、在(2)的条件下,是否存在t的值,使以P、B、D为顶点的三角形与△ABC相似;若存在,求t的值;若不存在,请说明理由.