2017年新疆昌吉州阜康市中考数学一模试卷
试卷更新日期：2017-04-19 类型：中考模拟
一、选择题
-
1. ±2是4的（ ）A、平方根 B、算术平方根 C、绝对值 D、相反数2. 晋商大院的许多窗格图案蕴含着对称之美，现从中选取以下四种窗格图案，其中是中心对称图形但不是轴对称图形的是（ ）A、
B、
C、
D、
3. 下列命题中，真命题是（ ）A、六边形的内角和为540度 B、多边形的外角和与边数有关 C、矩形的对角线互相垂直 D、三角形两边的和大于第三边4. 如果式子 有意义，那么x的取值范围在数轴上表示出来，正确的是（ ）A、
B、
C、
D、
5.某企业为了解员工给灾区“爱心捐款”的情况，随机抽取部分员工的捐款金额整理绘制成如图所示的直方图，根据图中信息，下列结论错误的是（ ）
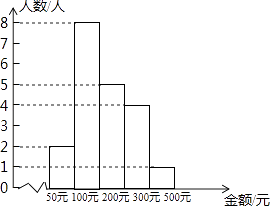A、样本中位数是200元 B、样本容量是20 C、该企业员工捐款金额的平均数是180元 D、该企业员工最大捐款金额是500元6. ▱ABCD中，对角线AC与BD交于点O，∠DAC=42°，∠CBD=23°，则∠COD是（ ）
A、61° B、63° C、65° D、67°7. 如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是（ ）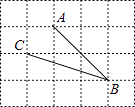
A、2 B、 C、 D、8. 匀速地向一个容器内注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为一折线），这个容器的形状是下图中的（ ）
A、
B、
C、
D、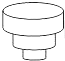
二、填空题
-
9. 计算（ + ）（ ﹣ ）的结果为 ．10. 不等式组 的最小整数解是 ．11. 甲乙两地9月上旬的日平均气温如图所示，则甲乙两地这10天日平均气温方差大小关系为S甲2S乙2（填＞或＜）．
12. 若关于x的方程x2+3x+a=0有一个根为﹣1，则另一个根为 ．13.如图，港口A在观测站O的正东方向，OA=4km，某船从港口A出发，沿北偏东15°方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°的方向，则该船航行的距离（即AB的长）为
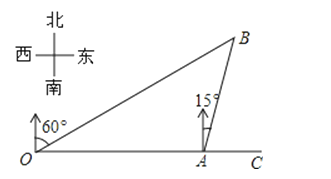14. 如图，在Rt△ABC中，∠C=30°，以直角顶点A为圆心，AB长为半径画弧交BC于点D，过D作DE⊥AC于点E．若DE=a，则△ABC的周长用含a的代数式表示为 ．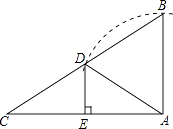
三、解答题
-
15. 先化简，再求值： ÷（1﹣ ），其中a= ﹣2．16. 如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．
17. 现代互联网技术的广泛应用．催生了快递行业的高速发展．据凋查，某家小型“大学生自主创业”的快递公司，今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件．现假定该公司每月的投递总件数的增长率相同．(1)、求该快递公司投递快递总件数的月平均增长率．(2)、如果平均每人每月最多可投递快递0.6万件，那么该公司现有的26名快递投递业务员能否完成今年6月份的快递投递任务？如果不能，请问至少需要增加几名业务员？18. 水龙头关闭不严会造成滴水，容器内盛水量w（L）与滴水时间t（h）的关系用可以显示水量的容器做如图1的试验，并根据试验数据绘制出如图2的函数图象，结合图象解答下列问题．
(1)、容器内原有水多少升？(2)、求w与t之间的函数关系式，并计算在这种滴水状态下一天的滴水量是多少升？19. 如图，菱形ABCD的对角线AC与BD相交于点O，且BE∥AC，CE∥BD．
(1)、求证：四边形OBEC是矩形；(2)、若菱形ABCD的周长是4 ，tanα= ，求四边形OBEC的面积．20. 某中学需在短跑、跳远、乒乓球、跳高四类体育项目中各选一名同学参加中学生运动会，根据平时成绩，把各项目进入复选的人员情况绘制成不完整的统计图、表如下：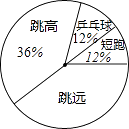
复选人员扇形统计图：
复选人员统计表：
项目/人数/性别
男
女
短跑
1
2
跳远
a
6
乒乓球
2
1
跳高
3
b
(1)、求a、b的值；(2)、求扇形统计图中跳远项目对应圆心角的度数；(3)、用列表法或画树状图的方法求在短跑和乒乓球项目中选出的两位同学都为男生的概率．
