2017年山东省潍坊市安丘市中考数学模拟试卷

试卷更新日期：2017-04-19 类型：中考模拟

进入出卷网下载

一、选择题

1. （ $- \frac{1}{8}$ ）的倒数是（）

A、 $\frac{1}{8}$ B、8 C、﹣8 D、﹣1

查看试题解析
2. 如图，是某几何体的三视图及相关数据，则该几何体的侧面积是（）

A、10π B、15π C、20π D、30π

查看试题解析
3. 下列运算正确的是（）

A、4a²﹣4a²=4a B、（﹣a³b）²=a⁶b² C、a+a=a² D、a²•4a⁴=4a⁸

查看试题解析
4. 如图，EF∥BC，AC平分∠BAF，∠B=80°，∠C=（）度．

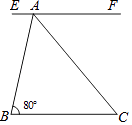A、40 B、45 C、50 D、55

查看试题解析
5. 下列运算正确的是（）

A、x³•x⁵=x¹⁵ B、（x²）⁵=x⁷ C、 $\sqrt[3]{27}$ =3 D、 $\frac{- a + b}{a + b}$ =﹣1

查看试题解析
6. 三角形的两边长分别为3和6，第三边的长是方程x²﹣6x+8=0的一个根，则这个三角形的周长是（）

A、9 B、11 C、13 D、11或13

查看试题解析
7. 若关于x的一元一次不等式组 ${\begin{matrix} x - 2 m < 0 \\ x + m > 2 \end{matrix}$ 有解，则m的取值范围为（）

A、 $m > - \frac{2}{3}$ B、m≤ $\frac{2}{3}$ C、m＞ $\frac{2}{3}$ D、m≤ $- \frac{2}{3}$

查看试题解析
8. 把直线y=﹣x+3向上平移m个单位后，与直线y=2x+4的交点在第一象限，则m的取值范围是（）

A、1＜m＜7 B、3＜m＜4 C、m＞1 D、m＜4

查看试题解析
9. 估计 $\frac{\sqrt{5} + 1}{2}$ 介于之间．（）

A、1.4与1.5 B、1.5与1.6 C、1.6与1.7 D、1.7与1.8

查看试题解析
10. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）

A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE

查看试题解析
11. 要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为（）

A、288° B、144° C、216° D、120°

查看试题解析
12. 已知二次函数y=ax²+bx+1（a＜0）的图象过点（1，0）和（x₁ ， 0），且﹣2＜x₁＜﹣1，下列5个判断中：①b＜0；②b﹣a＜0；③a＞b﹣1；④a＜﹣ $\frac{1}{2}$ ；⑤2a＜b+ $\frac{1}{2}$ ，正确的是（）

A、①③ B、①②③ C、①②③⑤ D、①③④⑤

查看试题解析

二、填空题

13. 如图：△ABC中，AB=AC，内切圆⊙O与边BC、AB分别切于点D、E、F，若∠C=30°，CE=2 $\sqrt{3}$ ，则AC= ．

查看试题解析
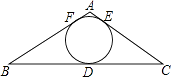14. 因式分解：﹣2x²y+12xy﹣16y= ．

查看试题解析
15. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} m x + n y = 7 \\ n x - m y = 1 \end{matrix}$ 的解，则m+3n的立方根为．

查看试题解析
16. 如图，将△ABC沿BC方向平移2cm得到△DEF，若△ABC的周长为16cm，则四边形ABFD的周长为．

查看试题解析
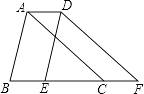17. 如图，在平面直角坐标系xOy中，四边形ODEF和四边形ABCD都是正方形，点F在x轴的正半轴上，点C在边DE上，反比例函数y= $\frac{k}{x}$ （k≠0，x＞0）的图象过点B，E．若AB=2，则k的值为．

查看试题解析
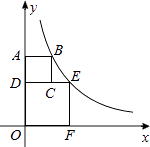18.
如图四边形ABCD中，AD=DC，∠DAB=∠ACB=90°，过点D作DF⊥AC，垂足为F．DF与AB相交于E．设AB=15，BC=9，P是射线DF上的动点．当△BCP的周长最小时，DP的长为．

查看试题解析

三、解答题

19. 计算下列各题

(1)、计算：（ $\frac{1}{2}$ ）^﹣²﹣6sin30°﹣（ $\frac{1}{\sqrt{7} - \sqrt{5}}$ ）⁰+ $\sqrt{2}$ +| $\sqrt{2}$ ﹣ $\sqrt{3}$ |

(2)、化简：（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ）÷ $\frac{x - 4}{x}$ ，然后请自选一个你喜欢的x值，再求原式的值．

查看试题解析
20. 今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．

(1)、试问去年每吨大蒜的平均价格是多少元？

(2)、该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？

查看试题解析
21.
如图，一枚运载火箭从地面O处发射，当火箭到达A点时，从地面C处的雷达站测得AC的距离是6km，仰角是43°，1s后，火箭到达B点，此时测得仰角为45.5°，这枚火箭从点A到点B的平均速度是多少？（结果精确到0.01）

查看试题解析
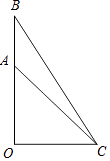22. 我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元．
经市场调研发现：该款工艺品每天的销售量y（件）与售价x（元）之间存在着如下表所示的一次函数关系．
售价x（元）
…
70
90
…
销售量y（件）
…
3000
1000
…
（利润=（售价﹣成本价）×销售量）

(1)、求销售量y（件）与售价x（元）之间的函数关系式；

(2)、你认为如何定价才能使工艺品厂每天获得的利润为40000元？

查看试题解析
23.
将△ABC绕点A按逆时针方向旋转θ度，并使各边长变为原来的n倍，得△AB′C′，如图①所示，∠BAB′=θ， $\frac{A B'}{A B}$ = $\frac{B' C'}{B C}$ = $\frac{A C'}{A C}$ =n，我们将这种变换记为[θ，n]．

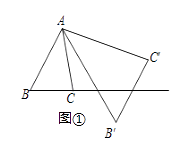(1)、
如图①，对△ABC作变换[60°， $\sqrt{3}$ ]得到△AB′C′，则S_△_AB'C：S_△_ABC=；直线BC与直线B′C′所夹的锐角为度；

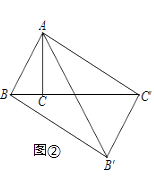
(2)、
如图②，△ABC中，∠BAC=30°，∠ACB=90°，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、C′在同一直线上，且四边形ABB′C′为矩形，求θ和n的值；

(3)、
如图③，△ABC中，AB=AC，∠BAC=36°，BC=1，对△ABC作变换[θ，n]得到△AB′C′，使点B、C、B′在同一直线上，且四边形ABB′C′为平行四边形，求θ和n的值．

查看试题解析

售价x（元）	…	70	90	…
销售量y（件）	…	3000	1000	…