2017年山东省聊城市冠县中考数学一模试卷
试卷更新日期:2017-04-19 类型:中考模拟
一、选择题
-
1. 在﹣ ,0,﹣2, ,1中,绝对值最大的数为( )A、0 B、﹣ C、﹣2 D、2. 下列计算正确的是( )A、2a2+4a2=6a4 B、(a+1)2=a2+1 C、(a2)3=a5 D、x7÷x5=x23. 为了实现街巷硬化工程高质量“全覆盖”,我省今年1﹣4月公路建设累计投资92.7亿元,该数据用科学记数法可表示为( )A、0.927×1010 B、92.7×1010 C、9.27×1011 D、9.27×1094. 函数y= 的自变量x的取值范围是( )A、x≥0且x≠2 B、x≥0 C、x≠2 D、x>25. 下列事件中,必然事件是( )A、掷一枚硬币,正面朝上 B、任意三条线段可以组成一个三角形 C、投掷一枚质地均匀的骰子,掷得的点数是奇数 D、13人中至少有两个人出生的月份相同6. 如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为( )
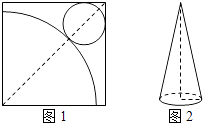 A、 cm B、4cm C、 cm D、 cm7. 如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是( )
A、 cm B、4cm C、 cm D、 cm7. 如图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中小正方形顶点A,B围成的正方体上的距离是( ) A、0 B、1 C、 D、8. 已知(x1 , y1),(x2 , y2),(x3 , y3)是反比例函数 的图象上的三个点,且x1<x2<0,x3>0,则y1 , y2 , y3的大小关系是( )A、y3<y1<y2 B、y2<y1<y3 C、y1<y2<y3 D、y3<y2<y19. 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数y= 在同一坐标系内的大致图象是( )
A、0 B、1 C、 D、8. 已知(x1 , y1),(x2 , y2),(x3 , y3)是反比例函数 的图象上的三个点,且x1<x2<0,x3>0,则y1 , y2 , y3的大小关系是( )A、y3<y1<y2 B、y2<y1<y3 C、y1<y2<y3 D、y3<y2<y19. 已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数y= 在同一坐标系内的大致图象是( )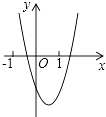 A、
A、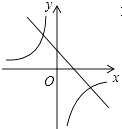 B、
B、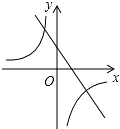 C、
C、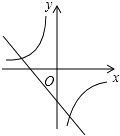 D、
D、 10. 关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k>1 C、k≠0 D、k>﹣1且k≠011. 某超市货架上摆放着桶装方便面,如图是它们的三视图,则货架上的桶装方便面至少有( )
10. 关于x的一元二次方程kx2+2x﹣1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k>1 C、k≠0 D、k>﹣1且k≠011. 某超市货架上摆放着桶装方便面,如图是它们的三视图,则货架上的桶装方便面至少有( )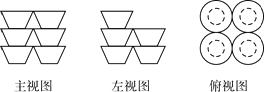 A、8桶 B、9桶 C、10桶 D、11桶12. 如图,直线y=﹣x+5与双曲线y= (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是 .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= (x>0)的交点有( )
A、8桶 B、9桶 C、10桶 D、11桶12. 如图,直线y=﹣x+5与双曲线y= (x>0)相交于A,B两点,与x轴相交于C点,△BOC的面积是 .若将直线y=﹣x+5向下平移1个单位,则所得直线与双曲线y= (x>0)的交点有( ) A、0个 B、1个 C、2个 D、0个,或1个,或2个
A、0个 B、1个 C、2个 D、0个,或1个,或2个二、填空题
-
13. 计算:2sin60°+2﹣1﹣20170﹣|1﹣ |= .14. 因式分解:6(x﹣3)2﹣24= .15. 在盒子里放有三张分别写有整式a+1、a+2、2的卡片,从中随机抽取两张卡片,把两张卡片上的整式分别作为分子和分母,则能组成分式的概率是 .16. 现定义运算“★”,对于任意实数a、b,都有a★b=a2﹣3a+b,如:3★5=32﹣3×3+5,若x★2=6,则实数x的值是 .17.
如图所示,直线y=x+1与y轴相交于点A1 , 以OA1为边作正方形OA1B1C1 , 记作第一个正方形;然后延长C1B1与直线y=x+1相交于点A2 , 再以C1A2为边作正方形C1A2B2C2 , 记作第二个正方形;同样延长C2B2与直线y=x+1相交于点A3 , 再以C2A3为边作正方形C2A3B3C3 , 记作第三个正方形;…,依此类推,则第n个正方形的边长为 .
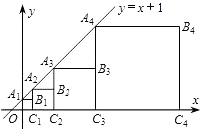
三、解答题
-
18. 计算下列各题(1)、 ﹣1=(2)、2x2+3=7x.19. 解方程(1)、先化简:(1﹣ )• ,再从1,2,3中选取的一个合适的数代入求值.(2)、求不等式组 的整数解.20. 某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元,求这两次各购进这种衬衫多少件?21. 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半小时后返回A地.如图是他们离A地的距离y(千米)与时间x(时)之间的函数关系图象.
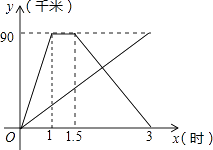 (1)、求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?22. 如图,已知一次函数y=x﹣2与反比例函数y= 的图象交于A、B两点.
(1)、求甲从B地返回A地的过程中,y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?22. 如图,已知一次函数y=x﹣2与反比例函数y= 的图象交于A、B两点. (1)、求A、B两点的坐标;(2)、观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;(3)、坐标原点为O,求△AOB的面积.23. 为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
(1)、求A、B两点的坐标;(2)、观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;(3)、坐标原点为O,求△AOB的面积.23. 为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.组别
分组
频数
频率
1
50≤x<60
9
0.18
2
60≤x<70
a
3
70≤x<80
20
0.40
4
80≤x<90
0.08
5
90≤x≤100
2
b
合计
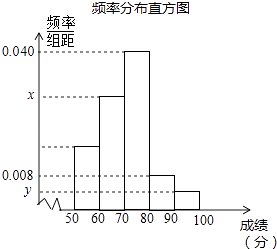
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)、求出a、b、x、y的值;(2)、若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)24. 某食品批发部准备用10000元从厂家购进一批出厂价分别为16元和20元的甲、乙两种酸奶,然后将甲、乙两种酸奶分别加价20%和25%向外销售.如果设购进甲种酸奶为x(箱),全部售出这批酸奶所获销售利润为y(元).(1)、求所获销售利润y(元)与x(箱)之间的函数关系式;(2)、根据市场调查,甲、乙两种酸奶在保质期内销售量都不超过300箱,那么食品批发部怎样进货获利最大,最大销售利润是多少?25. 如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).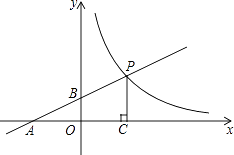 (1)、求双曲线的解析式;(2)、若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
(1)、求双曲线的解析式;(2)、若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.