2017年山东省济宁市中考数学模拟试卷
试卷更新日期:2017-04-19 类型:中考模拟
一、选择题
-
1. 的绝对值的相反数是( )A、 B、 C、2 D、﹣22. 环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了PM2.5检测指标,“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为( )A、2.5×10﹣5 B、2.5×105 C、2.5×10﹣6 D、2.5×1063. 下列运算正确的是( )A、(ab)5=ab5 B、a8÷a2=a6 C、(a2)3=a5 D、(a﹣b)5=a5﹣b54. 如图所示的几何体是由5个大小相同的小立方块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,l1∥l2 , ∠1=56°,则∠2的度数为( )
5. 如图,l1∥l2 , ∠1=56°,则∠2的度数为( )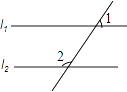 A、34° B、56° C、124° D、146°6. 平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )A、(﹣2,﹣3) B、(2,﹣3) C、(﹣3,﹣2) D、(3,﹣2)7. 分式方程 =1的解为( )A、x=﹣2 B、x=﹣3 C、x=2 D、x=38. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差s2如表所示:
A、34° B、56° C、124° D、146°6. 平面直角坐标系中,点P(﹣2,3)关于x轴对称的点的坐标为( )A、(﹣2,﹣3) B、(2,﹣3) C、(﹣3,﹣2) D、(3,﹣2)7. 分式方程 =1的解为( )A、x=﹣2 B、x=﹣3 C、x=2 D、x=38. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛,各组的平时成绩的平均数 (单位:分)及方差s2如表所示:甲
乙
丙
丁
7
8
8
7
s2
1
1.2
1
1.8
如果要选出一个成绩较好且状态稳定的组去参赛,那么应选的组是( )
A、甲 B、乙 C、丙 D、丁9. 二次函数y=2x2﹣3的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )A、抛物线开口向下 B、抛物线经过点(2,3) C、抛物线的对称轴是直线x=1 D、抛物线与x轴有两个交点10. 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )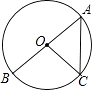 A、 π B、 π C、 π D、 π
A、 π B、 π C、 π D、 π二、填空题
-
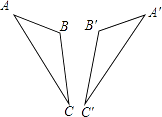
11. 已知|a+2|=0,则a= .12. 如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B= .
 13. 已知P1(x1 , y1),P2(x2 , y2)两点都在反比例函数y= 的图象上,且x1<x2<0,则y1y2(填“>”或“<”).14. 如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为 .
13. 已知P1(x1 , y1),P2(x2 , y2)两点都在反比例函数y= 的图象上,且x1<x2<0,则y1y2(填“>”或“<”).14. 如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为 . 15. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB= .
15. 如图,△ABC内接于⊙O,AH⊥BC于点H,若AC=24,AH=18,⊙O的半径OC=13,则AB= .
三、解答题
-
16. 计算:(﹣2)3+ ﹣2sin30°+(2016﹣π)0 .17. 先化简,再求代数式( ﹣ )÷ 的值,其中x=2sin60°﹣1,y=tan45°.18.
在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
 19. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张.
19. 在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示正整数后,背面朝上,洗匀放好,现从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张. (1)、请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);(2)、我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.20. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?21. 已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.(1)、如图1,求证:DE=DF;
(1)、请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果(卡片用A,B,C,D表示);(2)、我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,求抽到的两张卡片上的数都是勾股数的概率.20. 六•一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.(1)、求A、B两种品牌服装每套进价分别为多少元?(2)、该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?21. 已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.(1)、如图1,求证:DE=DF;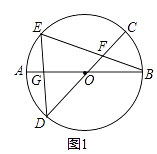 (2)、如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形;
(2)、如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形;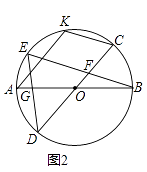 (3)、如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2 ,BE=4 ,求DH的长.
(3)、如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2 ,BE=4 ,求DH的长.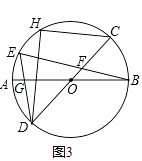 22. 如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣ ),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧.
22. 如图,在平面直角坐标系xOy中,抛物线y=a(x+1)2﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C(0,﹣ ),顶点为D,对称轴与x轴交于点H,过点H的直线l交抛物线于P,Q两点,点Q在y轴的右侧. (1)、求a的值及点A,B的坐标;(2)、当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;(3)、当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.
(1)、求a的值及点A,B的坐标;(2)、当直线l将四边形ABCD分为面积比为3:7的两部分时,求直线l的函数表达式;(3)、当点P位于第二象限时,设PQ的中点为M,点N在抛物线上,则以DP为对角线的四边形DMPN能否为菱形?若能,求出点N的坐标;若不能,请说明理由.