2017年山东省济宁市三维斋中考数学一模试卷

试卷更新日期：2017-04-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列图案中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中是必然事件的是（）

A、明天太阳从西边升起 B、篮球队员在罚球线上投篮一次，未投中 C、抛出一枚硬币，落地后正面朝上 D、实心铁球投入水中会沉入水底

查看试题解析
3. 下面如图是一个圆柱体，则它的正视图是（）

A、 B、 C、 D、

查看试题解析
4. 如果α是锐角，且sinα= $\frac{3}{5}$ ，那么cos（90°﹣α）的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
5. 如图，四边形ABCD为⊙O的内接四边形，E是BC延长线上的一点，已知∠BOD=100°，则∠DCE的度数为（）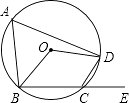

A、40° B、60° C、50° D、80°

查看试题解析
6. 如图，在△ABC中，两条中线BE，CD相交于点O，则S_△_DOE：S_△_COB等于（）

A、1：2 B、1：3 C、1：4 D、2：3

查看试题解析
7. 在下列网格中，小正方形的边长为1，点A，B，O都在格点上，求∠A的余弦值（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{10}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{1}{2}$

查看试题解析
8. 抛物线y=﹣2x²+1的对称轴是（）

A、直线x= $\frac{1}{2}$ B、直线x=﹣ $\frac{1}{2}$ C、直线x=2 D、y轴

查看试题解析
9. 为解决群众看病贵的问题，有关部门决定降低药价，对某种原价为289元的药品进行连续两次降价后为256元，设平均每次降价的百分率为x，则下面所列方程正确的是（）

A、289（1﹣x）²=256 B、256（1﹣x）²=289 C、289（1﹣2x）=256 D、256（1﹣2x）=289

查看试题解析
10. 如图，⊙O的半径为5，弦AB长为8，过AB的中点E有一动弦CD（点C只在 $\hat{A B}$ 上运动，且不与A、B重合），设EC=x，ED=y，下列能够表示y与x之间函数关系的图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 解方程x²﹣6x+5=0的解为．

查看试题解析
12. 在平面直角坐标系中，点A是抛物线y=a（x﹣3）²+k与y轴的交点，点B是这条抛物线上的另一点，且AB∥x轴，则以AB为边的等边三角形ABC的周长为．

查看试题解析
13. 如图所示，△ABC中，DE是BC的垂直平分线，DE交AC于点E，连接BE，若BE=13，BC=10，则sinC= ．

查看试题解析
14. 抛物线的顶点为P（﹣2，2），与y轴交于点A（0，3），若平移该抛物线使其顶点移动到点P₁（2，﹣2），那么得到的新抛物线的一般式是．

查看试题解析
15. 如图，已知在Rt△ABC中，AB=AC=3 $\sqrt{2}$ ，在△ABC内作第一个内接正方形DEFG；然后取GF的中点P，连接PD、PE，在△PDE内作第二个内接正方形HIKJ；再取线段KJ的中点Q，在△QHI内作第三个内接正方形…依次进行下去，则第2014个内接正方形的边长为．

查看试题解析

三、解答题

16. 计算下列各式

(1)、2cos45°+sin30°cos60°+cos30°

(2)、| $\sqrt{3}$ ﹣5|+2cos30°+（ $\frac{1}{3}$ ）^﹣¹+（9﹣ $\sqrt{3}$ ）⁰+ $\sqrt{4}$ ．

查看试题解析
17.
我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示，BC∥AD，斜坡AB=40米，坡角∠BAD=60°，为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造，经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡，改造时保持坡脚A不动，从坡顶B沿BC削进到E处，问BE至少是多少米？（结果保留根号）．

查看试题解析
18. 如图，反比例函数y= $\frac{4}{x}$ 的图象与一次函数y=kx﹣3的图象在第一象限内相交于点A，且点A的横坐标为4．

(1)、求点A的坐标及一次函数的解析式；

(2)、若直线x=2与反比例函数和一次函数的图象分别交于点B、C，求线段BC的长．

查看试题解析
19. 一个不透明的口袋里装有分别标有汉字“幸”、“福”、“济”、“宁”的四个小球，除汉字不同之外，小球没有任何区别，每次摸球前先搅拌均匀再摸球．

(1)、若从中任取一个球，球上的汉字刚好是“福”的概率为多少？

(2)、小颖从中任取一球，记下汉字后放回袋中，然后再从中任取一球，求小颖取出的两个球上汉字恰能组成“幸福”或“济宁”的概率．

查看试题解析
20. 如图，AB为⊙O的直径，AE为⊙O的切线，若tan∠ABE= $\frac{1}{2}$ ，AE=3，求BD的长．

查看试题解析
21. 如图，在菱形ABCD中，AB=2，∠ABC=60°，对角线AC、BD相交于点O，将对角线AC所在的直线绕点O顺时针旋转角α（0°＜α＜90°）后得直线l，直线l与AD、BC两边分别相交于点E和点F．

(1)、求证：△AOE≌△COF；

(2)、当α=30°时，求线段EF的长度．

查看试题解析
22.
如图，已知抛物线经过点A（2，0）和B（t，0）（t≥2），与y轴交于点C，直线l：y=x+2t经过点C，交x轴于点D，直线AE交抛物线于点E，且有∠CAE=∠CDO，作CF⊥AE于点F．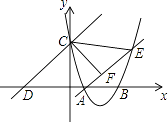

(1)、求∠CDO的度数；

(2)、求出点F坐标的表达式（用含t的代数式表示）；

(3)、当S_△_COD﹣S_四边形_COAF=7时，求抛物线解析式；

(4)、当以B，C，O三点为顶点的三角形与△CEF相似时，请直接写出t的值．

查看试题解析