2017年山东省济宁市嘉祥县中考数学一模试卷

试卷更新日期：2017-04-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列各对数是互为倒数的是（）

A、4和﹣4 B、﹣3和 $\frac{1}{3}$ C、﹣2和- $\frac{1}{2}$ D、0和0

查看试题解析
2. 下列计算结果正确的是（）

A、2a³+a³=3a⁶ B、（﹣a）²•a³=﹣a⁶ C、（﹣ $\frac{1}{2}$ ）^﹣²=4 D、（﹣2）⁰=﹣1

查看试题解析
3. 函数 $y = \sqrt{3 - x} + \frac{1}{x - 4}$ 的自变量x的取值范围是（）

A、x≤3 B、x≠4 C、x≥3且x≠4 D、x≤3或x≠4

查看试题解析
4. 如图，把一块含有30°角（∠A=30°）的直角三角板ABC的直角顶点放在矩形桌面CDEF的一个顶点C处，桌面的另一个顶点F与三角板斜边相交于点F，如果∠1=40°，那么∠AFE=（）

A、50° B、40° C、20° D、10°

查看试题解析
5. 如图，在▱ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于 $\frac{1}{2}$ EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（）

A、AG平分∠DAB B、AD=DH C、DH=BC D、CH=DH

查看试题解析
6. 甲、乙两名同学某学期的四次数学测试成绩（单位：分）如下表：
第一次
第二次
第三次
第四次
甲
87
95
85
93
乙
80
80
90
90
据上表计算，甲、乙两名同学四次数学测试成绩的方差分别为S_甲²=17、S_乙²=25，下列说法正确的是（）

A、甲同学四次数学测试成绩的平均数是89分 B、甲同学四次数学测试成绩的中位数是90分 C、乙同学四次数学测试成绩的众数是80分 D、乙同学四次数学测试成绩较稳定

查看试题解析
7. 如图，按照三视图确定该几何体的侧面积是（图中尺寸单位：cm）（）

A、40πcm² B、65πcm² C、80πcm² D、105πcm²

查看试题解析
8. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB=30°，CD=2 $\sqrt{3}$ ，则阴影部分的面积为（）

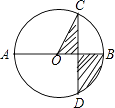A、2π B、π C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
9.
如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）

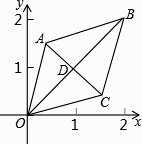A、（1，﹣1） B、（﹣1，﹣1） C、（ $\sqrt{2}$ ，0） D、（0，﹣ $\sqrt{2}$ ）

查看试题解析

二、填空题

10. 每到四月，许多地方杨絮、柳絮如雪花般漫天飞舞，人们不堪其扰，据测定，杨絮纤维的直径约为0.0000105m，该数值用科学记数法表示为．

查看试题解析
11. 已知m是关于x的方程x²﹣2x﹣3=0的一个根，则2m²﹣4m= ．

查看试题解析
12. 关于x的方程 $\frac{2 x + a}{x - 1} = 1$ 的解是正数，则a的取值范围是．

查看试题解析
13. 如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y= $\frac{3}{x}$ 的图象经过A，B两点，则菱形ABCD的面积为．

查看试题解析
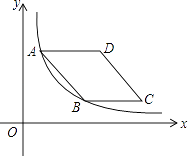14. 如图，坐标平面上，二次函数y=﹣x²+4x﹣k的图形与x轴交于A，B两点，与y轴交于C点，其顶点为D，且k＞0，若△ABC与△ABD的面积比为1：4，则k的值为．

查看试题解析

三、解答题

15. 先化简，再求值
（a﹣ $\frac{a^{2}}{a + b}$ ）（ $\frac{a}{a + b}$ ﹣1）÷ $\frac{b}{a + b}$ ，其中a，b分别为关于x的一元二次方程x²﹣ $\sqrt{3}$ x+1=0的两个根．

查看试题解析
16. 图①是小明在健身器材上进行仰卧起坐锻炼时的情景，图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图．已知AC=0.66米，BD=0.26米，α=20°．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364）

(1)、求AB的长（精确到0.01米）；

(2)、若测得ON=0.8米，试计算小明头顶由N点运动到M点的路径 $\overset{⌢}{M N}$ 的长度．（结果保留π）

查看试题解析
17. 为全面开展“阳光大课间”活动，某中学三个年级准备成立“足球”、“篮球”、“跳绳”、“踢毽”四个课外活动小组，学校体育组根据七年级学生的报名情况（每人限报一项）绘制了两幅不完整的统计图（如图），
请根据以上信息，完成下列问题：

(1)、m= ， n= ，并将条形统计图补充完整；

(2)、根据七年级的报名情况，试问全校2000人中，大约有多少人报名参加足球活动小组？

(3)、根据活动需要，从“跳绳”小组的二男二女四名同学中随机选取两人到“踢毽”小组参加训练，请用列表或树状图的方法计算恰好选中一男一女两名同学的概率．

查看试题解析
18. 如图1，在正方形ABCD中，点E，F分别是边BC，AB上的点，且CE=BF，连接DE，过点E作EG⊥DE，使EG=DE，连接FG，FC．

(1)、请判断：FG与CE的数量关系是，位置关系是；

(2)、如图2，若点E、F分别是CB、BA延长线上的点，其它条件不变，（1）中结论是否仍然成立？请出判断判断并给予证明．

查看试题解析
19.
如图，已知AB是⊙O的直径，C是⊙O上一点，∠BAC的平分线交⊙O于点D，交⊙O的切线BE于点E，过点D作DF⊥AC，交AC的延长线于点F．

(1)、求证：DF是⊙O的切线；

(2)、若DF=3，DE=2，求 $\frac{B E}{A D}$ 的值．

查看试题解析
20. 华联商场一种商品标价为40元，试销中发现：①一件该商品打九折销售仍可获利20%，②每天的销售量y（件）与每件的销售价x（元）满足一次函数y=162﹣3x．

(1)、求该商品的进价为多少元？

(2)、在不打折的情况下，如果商场每天想要获得销售利润420元，每件商品的销售价应定为多少元？

(3)、在不打折的情况下，如果商场要想获得最大利润，每件商品的销售价定为多少元为最合适？最大销售利润为多少？

查看试题解析
21.
正方形OABC的边长为4，对角线相交于点P，抛物线L经过O、P、A三点，点E是正方形内的抛物线上的动点．

(1)、建立适当的平面直角坐标系，
①直接写出O、P、A三点坐标；
②求抛物线L的解析式；

(2)、求△OAE与△OCE面积之和的最大值．

查看试题解析

	第一次	第二次	第三次	第四次
甲	87	95	85	93
乙	80	80	90	90