2017年山东省济南市市中区中考数学一模试卷

试卷更新日期：2017-04-19 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的绝对值等于（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. 数字3300用科学记数法表示为（）

A、0.33×10⁴ B、3.3×10³ C、3.3×10⁴ D、33×10³

查看试题解析
3. 如图，直线a∥b，直线c与直线a，b相交，若∠1=56°，则∠2等于（）

A、24° B、34° C、56° D、124°

查看试题解析
4. 若2（a+3）的值与4互为相反数，则a的值为（）

A、 $\frac{1}{2}$ B、﹣5 C、﹣ $\frac{7}{2}$ D、﹣1

查看试题解析
5. 如图所示的几何体是由一个圆柱体和一个长方形组成的，则这个几何体的俯视图是（　　）

A、 B、 C、 D、

查看试题解析
6. 下列运算正确的是（）

A、x²+x³=x⁵ B、（x﹣2）²=x²﹣4 C、（x³）⁴=x⁷ D、2x²⋅x³=2x⁵

查看试题解析
7. 下面四个手机应用图标中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 实验学校九年级一班十名同学定点投篮测试，每人投篮六次，投中的次数统计如下：5，4，3，5，5，2，5，3，4，1，则这组数据的中位数，众数分别为（　　）

A、4，5 B、5，4 C、4，4 D、5，5

查看试题解析
9.
如图，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（）

A、先向左平移5个单位，再向下平移2个单位 B、先向右平移5个单位，再向下平移2个单位 C、先向左平移5个单位，再向上平移2个单位 D、先向右平移5个单位，再向上平移2个单位

查看试题解析
10. 化简 $\frac{m - 1}{m}$ ÷ $\frac{1 - m}{m^{2}}$ 是（）

A、m B、﹣m C、 $\frac{1}{m}$ D、﹣ $\frac{1}{m}$

查看试题解析
11. 如图，直线l经过第二、三、四象限，l的解析式是y=（m﹣2）x+n，则m的取值范围在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
12. 如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于点E，则sin∠E的值是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
13. 已知关于x的二元一次方程组 ${\begin{matrix} 3 x + y = 3 m - 5 \\ x - y = m - 1 \end{matrix}$ ，若x+y＞3，则m的取值范围是（）

A、m＞1 B、m＜2 C、m＞3 D、m＞5

查看试题解析
14. 对于实数x，我们规定[x]表示不大于x的最大整数，如[4]=4，[ $\sqrt{3}$ ]=1，[﹣2.5]=﹣3．现对82进行如下操作：
82 $\overset{第 1 次}{\to}$ [ $\frac{82}{\sqrt{82}}$ ]=9 $\overset{第 2 次}{\to}$ [ $\frac{9}{3}$ ]=3 $\overset{第 3 次}{\to}$ [ $\frac{3}{\sqrt{3}}$ ]=1，这样对82只需进行3次操作后变为1，类似地，对121只需进行多少次操作后变为1（）

A、1 B、2 C、3 D、4

查看试题解析
15.
如图，直线y= $\frac{1}{2} x + 2$ 与y轴交于点A，与直线y=﹣ $\frac{1}{2} x$ 交于点B，以AB为边向右作菱形ABCD，点C恰与原点O重合，抛物线y=（x﹣h）²+k的顶点在直线y=﹣ $\frac{1}{2} x$ 上移动．若抛物线与菱形的边AB、BC都有公共点，则h的取值范围是（）

A、﹣2 $\leq h \leq \frac{1}{2}$ B、﹣2≤h≤1 C、﹣1 $\leq h \leq \frac{3}{2}$ D、﹣1 $\leq h \leq \frac{1}{2}$

查看试题解析

二、填空题

16. 因式分解：xy²﹣4x= ．

查看试题解析
17.
小明把如图所示的平行四边形纸板挂在墙上，完飞镖游戏（每次飞镖均落在纸板上，且落在纸板的任何一个点的机会都相等），则飞镖落在阴影区域的概率是．

查看试题解析
18. 方程 $\frac{3}{x}$ = $\frac{2}{x - 2}$ 的解是．

查看试题解析
19. 如图，A．B是双曲线y= $\frac{k}{x}$ 上的两点，过A点作AC⊥x轴，交OB于D点，垂足为C．若△ADO的面积为1，D为OB的中点，则k的值为．

查看试题解析
20. 如图，将一张矩形纸片ABCD沿对角线BD折叠，点C的对应点为C′，再将所折得的图形沿EF折叠，使得点D和点A重合．若AB=3，BC=4，则折痕EF的长为

查看试题解析

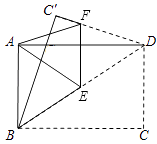
三、解答题

21. 解答题

(1)、先化简，再求值：（x+1）²+x（2﹣x），其中x= $\sqrt{2}$

(2)、解不等式组 ${\begin{matrix} 2 x - 4 < x \\ x + 9 > 4 x \end{matrix}$ ，并把解集表示在数轴上．

查看试题解析
22. 如图，C是AB的中点，AD=BE，CD=CE．求证：∠A=∠B．

查看试题解析
23. 如图，⊙O是△ABC的外接圆，∠A=45°，BD是直径，且BC=2，连接CD，求BD的长．

查看试题解析
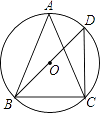24. 如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？

查看试题解析
25. 商店只有雪碧、可乐、果汁、奶汁四种饮料，某同学去该店购买饮料，每种饮料被选中的可能性相同．

(1)、若他去买一瓶饮料，则他买到奶汁的概率是多少？

(2)、若他两次去买饮料，每次买一瓶，且两次所买饮料品种不同，请用树状图或列表法求出他恰好买到雪碧和奶汁的概率．

查看试题解析
26.
如图1，已知双曲线y= $\frac{k}{x}$ （k＞0）与直线y=k′x交于A、B两点，点A在第一象限，试回答下列问题：

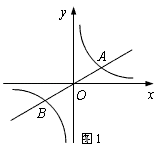(1)、若点A的坐标为（3，1），则点B的坐标为；当x满足：时， $\frac{k}{x}$ ≤k′x；

(2)、
如图2，过原点O作另一条直线l，交双曲线y= $\frac{k}{x}$ （k＞0）于P，Q两点，点P在第一象限．
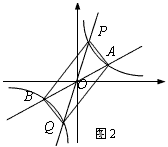
四边形APBQ一定是；

(3)、若点A的坐标为（3，1），点P的横坐标为1，求四边形APBQ的面积．

(4)、设点A，P的横坐标分别为m，n，四边形APBQ可能是矩形吗？可能是正方形吗？若可能，直接写出m，n应满足的条件；若不可能，请说明理由．

查看试题解析
27.
如图，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，点P为射线BD，CE的交点．

(1)、求证：BD=CE；

(2)、若AB=2，AD=1，把△ADE绕点A旋转，
①当∠EAC=90°时，求PB的长；
②直接写出旋转过程中线段PB长的最小值与最大值．

查看试题解析
28.
如图，二次函数y= $\frac{1}{2}$ x²+bx﹣ $\frac{3}{2}$ 的图象与x轴交于点A（﹣3，0）和点B，以AB为边在x轴上方作正方形ABCD，点P是x轴上一动点，连接DP，过点P作DP的垂线与y轴交于点E．

(1)、请直接写出点D的坐标：；

(2)、当点P在线段AO（点P不与A、O重合）上运动至何处时，线段OE的长有最大值，求出这个最大值；

(3)、是否存在这样的点P，使△PED是等腰三角形？若存在，请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积；若不存在，请说明理由．

查看试题解析