2017年山东省济南市历下区中考数学一模试卷
试卷更新日期:2017-04-19 类型:中考模拟
一、选择题
-
1. 4的平方根是( )A、±2 B、﹣2 C、2 D、2. 数值0.0000105用科学记数法表示为( )A、1.05×104 B、0.105×10﹣4 C、1.05×10﹣5 D、1.05×10﹣73. 下列计算正确的是( )A、a6÷a3=a3 B、(a2)3=a8 C、(a﹣b)2=a2﹣b2 D、a2+a2=a44. 如图,已知直线a、b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
 A、150° B、120° C、60° D、30°5. 下列标志中不是中心对称图形的是( )A、
A、150° B、120° C、60° D、30°5. 下列标志中不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 在平面直角坐标系中,点A的坐标为(1,2),将点A向右平移3个单位长度后得到A′,则点A′的坐标是( )A、(﹣2,2) B、(1,5) C、(1,﹣1) D、(4,2)7. 某多边形的内角和是其外角和的3倍,则此多边形的边数是( )A、5 B、6 C、7 D、88. 下列说法中,正确的是( )A、有一个角是直角的四边形是菱形 B、对角线互相垂直的菱形是正方形 C、对角线相等的平行四边形是矩形 D、一组邻边相等的平行四边形是正方形9. 化简 的结果是( )A、 B、 C、 D、10. 我省2014年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2016年的快递业务量达到4.5亿件.设2015年与2016年这两年的平均增长率为x,则下列方程正确的是( )A、1.4(1+x)=4.5 B、1.4(1+2x)=4.5 C、1.4(1+x)2=4.5 D、1.4(1+x)+1.4(1+x)2=4.511. 如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( )
6. 在平面直角坐标系中,点A的坐标为(1,2),将点A向右平移3个单位长度后得到A′,则点A′的坐标是( )A、(﹣2,2) B、(1,5) C、(1,﹣1) D、(4,2)7. 某多边形的内角和是其外角和的3倍,则此多边形的边数是( )A、5 B、6 C、7 D、88. 下列说法中,正确的是( )A、有一个角是直角的四边形是菱形 B、对角线互相垂直的菱形是正方形 C、对角线相等的平行四边形是矩形 D、一组邻边相等的平行四边形是正方形9. 化简 的结果是( )A、 B、 C、 D、10. 我省2014年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2016年的快递业务量达到4.5亿件.设2015年与2016年这两年的平均增长率为x,则下列方程正确的是( )A、1.4(1+x)=4.5 B、1.4(1+2x)=4.5 C、1.4(1+x)2=4.5 D、1.4(1+x)+1.4(1+x)2=4.511. 如图,矩形ABCD边AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于( ) A、1 B、2 C、3 D、412. 若式子 +(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是( )A、
A、1 B、2 C、3 D、412. 若式子 +(k﹣1)0有意义,则一次函数y=(k﹣1)x+1﹣k的图象可能是( )A、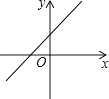 B、
B、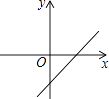 C、
C、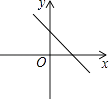 D、
D、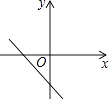 13. 已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值是( )A、1或﹣5 B、1或3 C、1或﹣3 D、﹣1或514. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
13. 已知二次函数y=(x﹣h)2+1(h为常数),在自变量x的值满足1≤x≤3的情况下,与其对应的函数值y的最小值为5,则h的值是( )A、1或﹣5 B、1或3 C、1或﹣3 D、﹣1或514. 在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足,设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )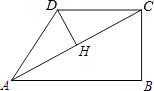 A、
A、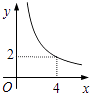 B、
B、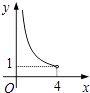 C、
C、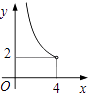 D、
D、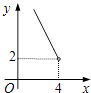 15. 如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1 , 当点C1、B1、C三点共线时,旋转角为α,连接BB1 , 交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1 , 其中正确的是( )
15. 如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1 , 当点C1、B1、C三点共线时,旋转角为α,连接BB1 , 交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1 , 其中正确的是( ) A、①③④ B、①②④ C、②③④ D、①②③④
A、①③④ B、①②④ C、②③④ D、①②③④二、填空题
-
16. 分解因式:x2﹣3x=17. 若分式 的值为0,则x的值为 .18. 如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是 .
 19. 若一元二次方程x2﹣2x+a=0有两个相等的实数根,则a的值是 .20. 如图,直线y=kx+b过A(﹣1,2),B(﹣2,0)两点,则0≤kx+b<4的解集为 .
19. 若一元二次方程x2﹣2x+a=0有两个相等的实数根,则a的值是 .20. 如图,直线y=kx+b过A(﹣1,2),B(﹣2,0)两点,则0≤kx+b<4的解集为 . 21. 如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An﹣1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y= (x>0)的图象于点B1、B2、B3、…、Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2 , …,若记△B1P1B2的面积为S1 , △B2P2B3的面积为S2 , …,△BnPnBn+1的面积为Sn , 则S1+S2+…+S2017= .
21. 如图,已知点A1、A2、A3、…、An在x轴上,且OA1=A1A2=A2A3═An﹣1An=1,分别过点A1、A2、A3、…、An作x轴的垂线,交反比例函数y= (x>0)的图象于点B1、B2、B3、…、Bn , 过点B2作B2P1⊥A1B1于点P1 , 过点B3作B3P2⊥A2B2于点P2 , …,若记△B1P1B2的面积为S1 , △B2P2B3的面积为S2 , …,△BnPnBn+1的面积为Sn , 则S1+S2+…+S2017= .
三、解答题
-
22. 计算下列各题(1)、计算:| |+( )﹣1﹣2cos45°(2)、解不等式组 ,并把解集在数轴上表示出来.23. 已知:如图,在▱ABCD中,延长AB到点E,使BE=AB,连接DE交BC于点F.求证:△BEF≌△CDF.
 24. 如图,在菱形ABCD中,对角线AC、BD相交于点O,已知AC=6,BD=8.求菱形ABCD的面积.
24. 如图,在菱形ABCD中,对角线AC、BD相交于点O,已知AC=6,BD=8.求菱形ABCD的面积. 25. 为改善生态环境,防止水土流失,2017年植树节前期某村计划在荒坡上种1200棵树,由于青年志愿者的支援,每天比原计划多种20%,结果提前5天完成任务,请问原计划每天种多少棵树?26. 如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值: ≈1.73, ≈1.41,结果精确到0.1米)
25. 为改善生态环境,防止水土流失,2017年植树节前期某村计划在荒坡上种1200棵树,由于青年志愿者的支援,每天比原计划多种20%,结果提前5天完成任务,请问原计划每天种多少棵树?26. 如图在数学活动课中,小敏为了测量小院内旗杆AB的高度,站在教学楼上的C处测得旗杆低端B的俯角为45°,测得旗杆顶端A的仰角为30°,如旗杆与教学楼的水平距离CD为12m,则旗杆AB的高度是多少米?(参考值: ≈1.73, ≈1.41,结果精确到0.1米) 27. 如图,正比例函数y=ax与反比例函数y= (x>0)的图象交于点M( , ).
27. 如图,正比例函数y=ax与反比例函数y= (x>0)的图象交于点M( , ). (1)、求这两个函数的表达式;(2)、如图1,若∠AMB=90°,且其两边分别于两坐标轴的正半轴交于点A、B.求四边形OAMB的面积.(3)、如图2,点P是反比例函数y= (x>0)的图象上一点,过点P作x轴、y轴的垂线,垂足分别为E、F,PF交直线OM于点H,过作x轴的垂线,垂足为G.设点P的横坐标为m,当m> 时,是否存在点P,使得四边形PEGH为正方形?若存在,求出P点的坐标;若不存在,请说明理由.28. 如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B.
(1)、求这两个函数的表达式;(2)、如图1,若∠AMB=90°,且其两边分别于两坐标轴的正半轴交于点A、B.求四边形OAMB的面积.(3)、如图2,点P是反比例函数y= (x>0)的图象上一点,过点P作x轴、y轴的垂线,垂足分别为E、F,PF交直线OM于点H,过作x轴的垂线,垂足为G.设点P的横坐标为m,当m> 时,是否存在点P,使得四边形PEGH为正方形?若存在,求出P点的坐标;若不存在,请说明理由.28. 如图,在△ABC中,已知CA=CB=5,BA=6,点E是线段AB上的动点(不与端点重合),点F是线段AC上的动点,连接CE、EF,若在点E、点F的运动过程中,始终保证∠CEF=∠B. (1)、求证:∠AEF=∠BCE;(2)、当以点C为圆心,以CF为半径的圆与AB相切时,求BE的长;(3)、探究:在点E、F的运动过程中,△CEF可能为等腰三角形吗?若能,求出BE的长;若不能,请说明理由.29. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(﹣1,0)、B(3,0).
(1)、求证:∠AEF=∠BCE;(2)、当以点C为圆心,以CF为半径的圆与AB相切时,求BE的长;(3)、探究:在点E、F的运动过程中,△CEF可能为等腰三角形吗?若能,求出BE的长;若不能,请说明理由.29. 如图1,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、点B(点A在点B左侧),与y轴交于点C,点D为抛物线的顶点,已知点A、点B的坐标分别为A(﹣1,0)、B(3,0). (1)、求抛物线的解析式;(2)、在直线BC上方的抛物线上找一点P,使△PBC的面积最大,求P点的坐标;(3)、如图2,连接BD、CD,抛物线的对称轴与x轴交于点E,过抛物线上一点M作MN⊥CD,交直线CD于点N,求当∠CMN=∠BDE时点M的坐标.
(1)、求抛物线的解析式;(2)、在直线BC上方的抛物线上找一点P,使△PBC的面积最大,求P点的坐标;(3)、如图2,连接BD、CD,抛物线的对称轴与x轴交于点E,过抛物线上一点M作MN⊥CD,交直线CD于点N,求当∠CMN=∠BDE时点M的坐标.