2017年江西省宜春市高安市中考数学一模试卷

试卷更新日期：2017-04-19 类型：中考模拟

进入出卷网下载

一、选择题

1. 在0，﹣2，1，5这四个数中，最小的数是（）

A、0 B、﹣2 C、1 D、5

查看试题解析
2. 下列三条线段不能构成三角形的三边的是（）

A、3cm，4cm，5cm B、5cm，6cm，11cm C、5cm，6cm，10cm D、2cm，3cm，4cm

查看试题解析
3. 已知sina= $\frac{\sqrt{3}}{2}$ ，且a是锐角，则a=（）

A、75° B、60° C、45° D、30°

查看试题解析
4. 为了调查瑞州市2016年初三年级学生的身高，从中抽取出200名学生进行调查，这个问题中样本容量为（）

A、被抽取的200名学生的身高 B、200 C、200名 D、初三年级学生的身高

查看试题解析
5. 平行四边形、矩形、正方形之间的关系是（）

A、 B、 C、 D、

查看试题解析
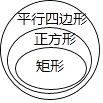6. 下面几何体的主视图是（）

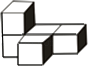A、 B、 C、 D、

查看试题解析

二、填空题

7. 2016年我市经济依然保持了平稳增长．据统计，截止到今年4月底，我市金融机构存款余额约为1193亿元，用科学记数法应记为元．

查看试题解析
8. 分解因式：a³﹣16a= ．

查看试题解析
9. 有两名学员小林和小明练习射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计小林和小明两人中新手是．

查看试题解析
10. 定义新运算“※”，规则：a※b=ab﹣a﹣b，如1※2=1×2﹣1﹣2=﹣1，若x²+x﹣1=0的两根为x₁ ， x₂ ，则x₁※x₂= ．

查看试题解析
11. 如图a是长方形纸带，∠DEF=20°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是度．

查看试题解析
12. 如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10CM，小圆半径为6CM，则弦AB的长为 CM．

查看试题解析

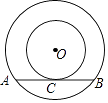
三、解答题

13. 计算下列各题

(1)、计算： $\sqrt{2}$ + ${(\frac{1}{2})}^{- 2}$ +（﹣1）⁰﹣2sin45°

(2)、求满足 ${\begin{matrix} 2 x + y = 15 \\ y + 7 x \leq 22 \end{matrix}$ 的x、y的正整数解．

查看试题解析
14. 如图，以AB为直径的⊙O交△ABC的BC、AC边与D、E两点，在图中仅以没有刻度的直尺画出三角形的三条高（简单叙述你的画法）．

查看试题解析
15. 先化简：（1+ $\frac{1}{x}$ ）÷ $\frac{x^{2} - 1}{x}$ ，再从1、﹣1、0、2中选择一个合适的数代入求值．

查看试题解析
16. 如图，已知△ABC中，AB=AC，BD、CE是高，BD与CE相交于点O

(1)、求证：OB=OC；

(2)、若∠ABC=50°，求∠BOC的度数．

查看试题解析
17. 甲、乙、丙、丁四人参加某校招聘教师考试，试后甲、乙两人去询问成绩．请你根据下面回答者对甲、乙两人回答的内容进行分析，

(1)、列举出这四人的名次排列所有可能出现的不同情况．

(2)、求甲排在第一名的概率？

查看试题解析
18. 如图，在3×3的方阵图中，填写了一些数和代数式（其中每个代数式都表示一个数），使得每行的3个数、每列的3个数、斜对角的3个数之和均相等．
3
4
x
﹣2
y
a
2y﹣x
c
b
备用图
3
4

﹣2

(1)、求x，y的值；

(2)、在备用图中完成此方阵图．

查看试题解析
19.
一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．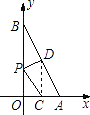

(1)、求该函数的解析式；

(2)、O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值，并求取得最小值时P点的坐标．

查看试题解析
20. 某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．

(1)、求商场经营该商品原来一天可获利润多少元？

(2)、设后来该商品每件降价x元，商场一天可获利润y元．
①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？
②求出y与x之间的函数关系式，并通过画该函数图象的草图，观察其图象的变化趋势，结合题意写出当x取何值时，商场获利润不少于2160元．

查看试题解析
21. 小明用下面的方法求出方程2 $\sqrt{x}$ ﹣3=0的解，请你仿照他的方法求出下面另外两个方程的解，并把你的解答过程填写在下面的表格中．
方程
换元法得新方程
解新方程
检验
求原方程的解
2 $\sqrt{x}$ ﹣3=0
令 $\sqrt{x}$ =t，则2t﹣3=0
t= $\frac{3}{2}$
t= $\frac{3}{2}$ ＞0
$\sqrt{x}$ = $\frac{3}{2}$ ，所以x= $\frac{9}{4}$
x﹣2 $\sqrt{x}$ +1=0
x+2+ $\sqrt{x + 2}$ =0

查看试题解析
22. 阅读下列材料，并解决后面的问题．
材料：我们知道，n个相同的因数a相乘 $\underset{n}{\underset{︸}{a \cdot a \dots a}}$ 可记为aⁿ ，如2³=8，此时，3叫做以2为底8的对数，记为log₂8（即log₂8=3），一般地，若aⁿ=b （a＞0且a≠1，b＞0），则n叫做以a为底b的对数，记为log_ab（即log_ab=n）．如3⁴=81，则4叫做以3为底81的对数，记为log₃81（即log₃81=4）

(1)、计算以下各对数的值：log₂4= ， log₂16= ， log₂64= ．

(2)、观察（1）中三数4、16、64之间满足怎样的关系式？log₂4、log₂16、log₂64之间又满足怎样的关系式？

(3)、根据（2）的结果，我们可以归纳出：log_aM+log_aN=log_aM N（a＞0且a≠1，M＞0，N＞0）
请你根据幂的运算法则：a^m=a^m⁺ⁿ以及对数的定义证明该结论．

查看试题解析
23.
如图，抛物线y=x²﹣2x﹣3与x轴交A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．

(1)、求A、B两点的坐标及直线AC的函数表达式；

(2)、P是线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值；

(3)、点G抛物线上的动点，在x轴上是否存在点F，使A、C、F、G这样的四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的F点坐标；如果不存在，请说明理由．

查看试题解析

方程	换元法得新方程	解新方程	检验	求原方程的解
2 $\sqrt{x}$ ﹣3=0	令 $\sqrt{x}$ =t，则2t﹣3=0	t= $\frac{3}{2}$	t= $\frac{3}{2}$ ＞0	$\sqrt{x}$ = $\frac{3}{2}$ ，所以x= $\frac{9}{4}$
x﹣2 $\sqrt{x}$ +1=0
x+2+ $\sqrt{x + 2}$ =0

3	4	x
﹣2	y	a
2y﹣x	c	b

3	4
﹣2