2017年江苏省苏州市昆山市中考数学一模试卷
试卷更新日期:2017-04-19 类型:中考模拟
一、选择题
-
1. 2017的相反数是( )A、2017 B、﹣2017 C、 D、﹣2. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1093. 下列计算正确的是( )A、3a+4b=7ab B、(ab3)2=ab6 C、(a+2)2=a2+4 D、x12÷x6=x64. 互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )A、120元 B、100元 C、80元 D、60元5. 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
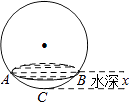 A、
A、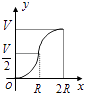 B、
B、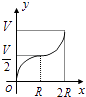 C、
C、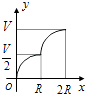 D、
D、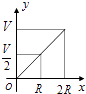 6. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
6. 如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )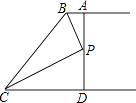 A、8 B、6 C、4 D、27. 直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )A、x≤3 B、x≥3 C、x≥﹣3 D、x≤08. 已知实数x,y满足 ,则以x,y的值为两边长的等腰三角形的周长是( )A、20或16 B、20 C、16 D、以上答案均不对9. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )A、k<5 B、k<5,且k≠1 C、k≤5,且k≠1 D、k>510. 已知直线y=﹣ x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣ (x﹣ )2+4上,能使△ABP为等腰三角形的点P的个数有( )A、3个 B、4个 C、5个 D、6个
A、8 B、6 C、4 D、27. 直线y=kx+3经过点A(2,1),则不等式kx+3≥0的解集是( )A、x≤3 B、x≥3 C、x≥﹣3 D、x≤08. 已知实数x,y满足 ,则以x,y的值为两边长的等腰三角形的周长是( )A、20或16 B、20 C、16 D、以上答案均不对9. 若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )A、k<5 B、k<5,且k≠1 C、k≤5,且k≠1 D、k>510. 已知直线y=﹣ x+3与坐标轴分别交于点A,B,点P在抛物线y=﹣ (x﹣ )2+4上,能使△ABP为等腰三角形的点P的个数有( )A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 在函数 中,自变量x的取值范围是 .12. 分解因式:ax2﹣ay2= .13. 某校男子足球队的年龄分布如图的条形图,请求出这些队员年龄的平均数、中位数
 14. 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是 .
14. 如图,在4×4正方形网格中,黑色部分的图形构成一个轴对称图形,现在任选取一个白色的小正方形并涂黑,使图中黑色部分的图形仍然构成一个轴对称图形的概率是 . 15. 在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为(用含a的式子表示).
15. 在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按下列方式折叠,若EF的长度为a,则△DEF的周长为(用含a的式子表示). 16. 关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负,则实数m的取值范围是 .17. 如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为 .
16. 关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为负,则实数m的取值范围是 .17. 如图,已知直线l:y=﹣x,双曲线y= ,在l上取一点A(a,﹣a)(a>0),过A作x轴的垂线交双曲线于点B,过B作y轴的垂线交l于点C,过C作x轴的垂线交双曲线于点D,过D作y轴的垂线交l于点E,此时E与A重合,并得到一个正方形ABCD,若原点O在正方形ABCD的对角线上且分这条对角线为1:2的两条线段,则a的值为 . 18. 将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象.若该图象在直线y=2下方的点的横坐标x满足0<x<3,则b的取值范围为 .
18. 将函数y=2x+b(b为常数)的图象位于x轴下方的部分沿x轴翻折至其上方后,所得的折线是函数y=|2x+b|(b为常数)的图象.若该图象在直线y=2下方的点的横坐标x满足0<x<3,则b的取值范围为 .三、解答题
-
19. 计算:20160﹣|﹣ |+ +2sin45°.20. 先化简,再求值:( ﹣x+1)÷ ,其中x= ﹣2.21. 解不等式组: ,并把解集在数轴上表示出来.22. 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》,这是中国足球历史上的重大改革.为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息,解答下列问题:
 (1)、a= , b= ,(2)、补全频数分布直方图;(3)、若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?(4)、在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.23. 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(1)、a= , b= ,(2)、补全频数分布直方图;(3)、若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?(4)、在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表我市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.23. 如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, (1)、求反比例函数y= 的解析式;(2)、求cos∠OAB的值;(3)、求经过C、D两点的一次函数解析式.24. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)、求反比例函数y= 的解析式;(2)、求cos∠OAB的值;(3)、求经过C、D两点的一次函数解析式.24. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. (1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.25. “世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.(1)、求今年6月份A型车每辆销售价多少元(用列方程的方法解答);(2)、该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
(1)、求证:△AEC≌△ADB;(2)、若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.25. “世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.顺风车行经营的A型车2015年6月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年6月份与去年6月份卖出的A型车数量相同,则今年6月份A型车销售总额将比去年6月份销售总额增加25%.(1)、求今年6月份A型车每辆销售价多少元(用列方程的方法解答);(2)、该车行计划7月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
26. 已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d= 计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= = = = .
根据以上材料,解答下列问题:
(1)、求点P(1,﹣1)到直线y=x﹣1的距离;(2)、已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= x+9的位置关系并说明理由;(3)、已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.27. 如图,在等腰直角三角形ABC中,∠BAC=90°,AC=8 cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以 cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2) (1)、当点M落在AB上时,x=;(2)、当点M落在AD上时,x=;(3)、求y关于x的函数解析式,并写出自变量x的取值范围.28. 已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣ x+b与抛物线的另一个交点为D.
(1)、当点M落在AB上时,x=;(2)、当点M落在AD上时,x=;(3)、求y关于x的函数解析式,并写出自变量x的取值范围.28. 已知抛物线y=a(x+3)(x﹣1)(a≠0),与x轴从左至右依次相交于A、B两点,与y轴相交于点C,经过点A的直线y=﹣ x+b与抛物线的另一个交点为D. (1)、若点D的横坐标为2,求抛物线的函数解析式;(2)、若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;(3)、在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?
(1)、若点D的横坐标为2,求抛物线的函数解析式;(2)、若在第三象限内的抛物线上有点P,使得以A、B、P为顶点的三角形与△ABC相似,求点P的坐标;(3)、在(1)的条件下,设点E是线段AD上的一点(不含端点),连接BE.一动点Q从点B出发,沿线段BE以每秒1个单位的速度运动到点E,再沿线段ED以每秒 个单位的速度运动到点D后停止,问当点E的坐标是多少时,点Q在整个运动过程中所用时间最少?