2017年湖南省娄底市中考数学模拟试卷(3月份)
试卷更新日期:2017-04-19 类型:中考模拟
一、选择题
-
1. 如图,双曲线y= 的一个分支为( )
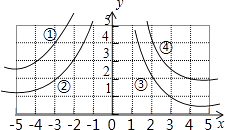 A、① B、② C、③ D、④2. 关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为( )A、﹣1 B、0 C、1 D、﹣1或13. 如图,DE∥BC,在下列比例式中,不能成立的是( )
A、① B、② C、③ D、④2. 关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为( )A、﹣1 B、0 C、1 D、﹣1或13. 如图,DE∥BC,在下列比例式中,不能成立的是( ) A、 B、 C、 D、4. 已知在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )A、 B、 C、 D、5. 函数y=﹣x2+1的图象大致为( )A、
A、 B、 C、 D、4. 已知在Rt△ABC中,∠C=90°,sinA= ,则tanB的值为( )A、 B、 C、 D、5. 函数y=﹣x2+1的图象大致为( )A、 B、
B、 C、
C、 D、
D、 6. 抛物线y=2(x﹣3)2的顶点在( )A、第一象限 B、第二象限 C、x轴上 D、y轴上7.
6. 抛物线y=2(x﹣3)2的顶点在( )A、第一象限 B、第二象限 C、x轴上 D、y轴上7.如图,AB为⊙O直径,CD为弦,AB⊥CD,如果∠BOC=70°,那么∠A的度数为( )
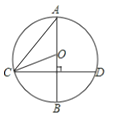 A、70° B、35° C、30° D、20°8. 把抛物线y=﹣2x2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( )A、y=﹣2(x﹣1)2+6 B、y=﹣2(x﹣1)2﹣6 C、y=﹣2(x+1)2+6 D、y=﹣2(x+1)2﹣69. 从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )A、0 B、 C、 D、110.
A、70° B、35° C、30° D、20°8. 把抛物线y=﹣2x2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( )A、y=﹣2(x﹣1)2+6 B、y=﹣2(x﹣1)2﹣6 C、y=﹣2(x+1)2+6 D、y=﹣2(x+1)2﹣69. 从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )A、0 B、 C、 D、110.如图所示的几何体的左视图是( )
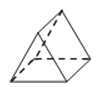 A、
A、 B、
B、 C、
C、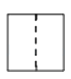 D、
D、 11. 关于x的方程x2﹣ax+2a=0的两根的平方和是5,则a的值是( )A、﹣1或5 B、1 C、5 D、﹣112. 如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( )
11. 关于x的方程x2﹣ax+2a=0的两根的平方和是5,则a的值是( )A、﹣1或5 B、1 C、5 D、﹣112. 如图,已知△ABC和△ADE均为等边三角形,D在BC上,DE与AC相交于点F,AB=9,BD=3,则CF等于( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 如图,点P在反比例函数y= 的图象上,且PD⊥x轴于点D.若△POD的面积为3,则k的值是 .
 14. 在Rt△ABC,若CD是Rt△ABC斜边AB上的高,AD=3,CD=4,则BC .15. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为米.
14. 在Rt△ABC,若CD是Rt△ABC斜边AB上的高,AD=3,CD=4,则BC .15. 如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高CD为米. 16. 若抛物线y=x2﹣2x﹣3与x轴分别交于A,B两点,则A,B的坐标为17. 若代数式x2﹣8x+12的值是21,则x的值是18. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作第1个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第2个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积是
16. 若抛物线y=x2﹣2x﹣3与x轴分别交于A,B两点,则A,B的坐标为17. 若代数式x2﹣8x+12的值是21,则x的值是18. 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作第1个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第2个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积是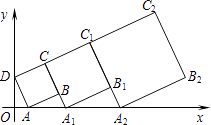
三、解答题
-
19. 关于x的一元二次方程x2﹣3x﹣k=0有两个不相等的实数根.(1)、求k的取值范围;(2)、请选择一个整数k值,使方程的两根同号,并求出方程的根.20. 计算: sin60°﹣4cos230°+sin45°•tan60°+( )﹣2 .
四、解答题
-
21.
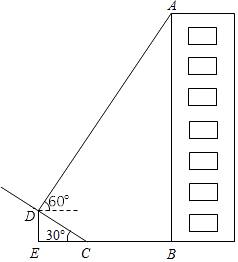
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为60°,已知坡角为30°,你能求出楼房AB的高度吗?
 22. 为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况.小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.
22. 为了解某中学学生对“厉行勤俭节约,反对铺张浪费”主题活动的参与情况.小强在全校范围内随机抽取了若干名学生并就某日午饭浪费饭菜情况进行了调查.将调查内容分为四组:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.根据调查结果,绘制了如图所示两幅尚不完整的统计图.
回答下列问题:
(1)、这次被抽查的学生共有人,扇形统计图中,“B组”所对应的圆心角的度数为;(2)、补全条形统计图;(3)、已知该中学共有学生2500人,请估计这日午饭有剩饭的学生人数;若按平均每人剩10克米饭计算,这日午饭将浪费多少千克米饭?五、解答题
-
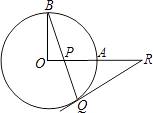
23. 如图,OA和OB是⊙O的半径,并且OA⊥OB,P是OA上任一点,BP的延长线交⊙O于Q,过Q的⊙O的切线交OA的延长线于R.求证:RP=RQ.
 24. 某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售单价25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.(1)、写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大;(3)、商场的营销部结合上述情况,提出了A、B两种营销方案:
24. 某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现:当销售单价25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.(1)、写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大;(3)、商场的营销部结合上述情况,提出了A、B两种营销方案:方案A:该文具的销售单价高于进价且不超过30元;
方案B:每件文具的利润不低于为25元且不高于29元.
请比较哪种方案的最大利润更高,并说明理由.
六、解答题
-
25.
已知抛物线y=ax2+bx+c的顶点为A,经过点B(0,3)和点(2,3),与x轴交于C,D两点,(点C在点D的左侧),且OD=OB.
 (1)、求这条抛物线的表达式;(2)、连接AB,BD,DA,试判断△ABD的形状;(3)、点P是BD上方抛物线上的动点,当P运动到什么位置时,△BPD的面积最大?求出此时点P的坐标及△BPD的面积.26. 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)、求这条抛物线的表达式;(2)、连接AB,BD,DA,试判断△ABD的形状;(3)、点P是BD上方抛物线上的动点,当P运动到什么位置时,△BPD的面积最大?求出此时点P的坐标及△BPD的面积.26. 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF. (1)、求证:直线PA为⊙O的切线;(2)、试探究线段EF、OD、OP之间的等量关系,并加以证明;(3)、若BC=6,tan∠F= ,求cos∠ACB的值和线段PE的长.
(1)、求证:直线PA为⊙O的切线;(2)、试探究线段EF、OD、OP之间的等量关系,并加以证明;(3)、若BC=6,tan∠F= ,求cos∠ACB的值和线段PE的长.