2019年高考数学二轮复习专题07:计数原理、程序框图、概率与统计
试卷更新日期:2019-02-21 类型:二轮复习
一、单选题
-
1. 设不等式组 表示的平面区域为 ,在区域 内随机取一个点,则此点到坐标原点的距离大于1的概率是( )A、
 B、
B、 C、
C、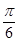 D、
D、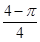 2. 如图所示的阴影部分是由 轴及曲线 围成,在矩形区域 内随机取一点,则该点取自阴影部分的概率是( )
2. 如图所示的阴影部分是由 轴及曲线 围成,在矩形区域 内随机取一点,则该点取自阴影部分的概率是( )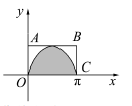 A、
A、 B、
C、
B、
C、 D、
D、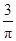 3. 下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为y=0.8x-155,后因某未知原因第五组数据的y值模糊不清,此位置数据记为m(如下所示),则利用回归方程可求得实数m的值为( )
3. 下列表格所示的五个散点,原本数据完整,且利用最小二乘法求得这五个散点的线性回归直线方程为y=0.8x-155,后因某未知原因第五组数据的y值模糊不清,此位置数据记为m(如下所示),则利用回归方程可求得实数m的值为( )x
196
197
200
203
204
y
1
3
6
7
m
A、8.3 B、8 C、8.1 D、8.24. 一个体积可忽略不计的小球在边长为2的正方形区域内随机滚动,则它在离4个顶点距离都大于1的区域内的概率为 ( )A、 B、 C、
C、 D、
5. 如图, 是 上一点,分别以 为直径作半圆.从 作 ,与半圆相交于 . ,在整个图形中随机取一点,则此点取自图中阴影部分的概率是( )
D、
5. 如图, 是 上一点,分别以 为直径作半圆.从 作 ,与半圆相交于 . ,在整个图形中随机取一点,则此点取自图中阴影部分的概率是( ) A、 B、 C、 D、6. 利用随机模拟方法可估计无理数 的数值,为此设计右图所示的程序框图,其中rand( )表示产生区间(0,1)上的随机数, 是 与 的比值,执行此程序框图,输出结果 的值趋近于 ( )
A、 B、 C、 D、6. 利用随机模拟方法可估计无理数 的数值,为此设计右图所示的程序框图,其中rand( )表示产生区间(0,1)上的随机数, 是 与 的比值,执行此程序框图,输出结果 的值趋近于 ( )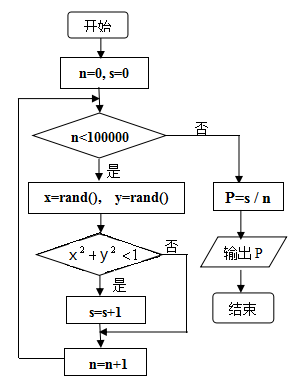 A、
A、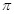 B、
B、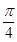 C、
C、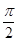 D、
D、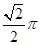 7. 一颗质地均匀的正方体骰子,其六个面上的点数分别为1,2,3,4,5,6,将这颗骰子连续抛掷三次,观察向上的点数,则三次点数依次构成等差数列的概率为( )A、 B、 C、
7. 一颗质地均匀的正方体骰子,其六个面上的点数分别为1,2,3,4,5,6,将这颗骰子连续抛掷三次,观察向上的点数,则三次点数依次构成等差数列的概率为( )A、 B、 C、 D、
D、 8. 在区间 上随机取一个数 ,则事件“ ”发生的概率为( )A、 B、
8. 在区间 上随机取一个数 ,则事件“ ”发生的概率为( )A、 B、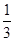 C、
D、
9. 记函数 的定义域为D,在区间 上随机取一个实数x,则 的概率是A、
C、
D、
9. 记函数 的定义域为D,在区间 上随机取一个实数x,则 的概率是A、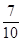 B、
B、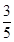 C、
C、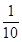 D、
D、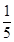 10. 为保证树苗的质量,林业管理部门在每年3月12日植树节前都对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度 单位长度: ,其茎叶图如图所示,则下列描述正确的是( )
10. 为保证树苗的质量,林业管理部门在每年3月12日植树节前都对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度 单位长度: ,其茎叶图如图所示,则下列描述正确的是( )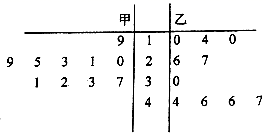 A、甲种树苗的平均高度大于乙种树苗的平均高度,甲种树苗比乙种树苗长得整齐 B、甲种树苗的平均高度大于乙种树苗的平均高度,乙种树苗比甲种树苗长得整齐 C、乙种树苗的平均高度大于甲种树苗的平均高度,乙种树苗比甲种树苗长得整齐 D、乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐
A、甲种树苗的平均高度大于乙种树苗的平均高度,甲种树苗比乙种树苗长得整齐 B、甲种树苗的平均高度大于乙种树苗的平均高度,乙种树苗比甲种树苗长得整齐 C、乙种树苗的平均高度大于甲种树苗的平均高度,乙种树苗比甲种树苗长得整齐 D、乙种树苗的平均高度大于甲种树苗的平均高度,甲种树苗比乙种树苗长得整齐二、填空题
-
11. 现有8本杂志,其中有3本是完全相同的文学杂志,还有5本是互不相同的数学杂志,从这8本里选取3本,则不同选法的种数为 .12. 的二项展开式中 的系数是 . (用数字作答)
13. 若采用随机模拟的方法估计某运动员射击击中目标的概率.先由计算器给出0到9之间取整数的随机数,指定0,1,2,3表示没有击中目标,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组如下的随机数:7327 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该运动员射击4次至少击中3次的概率为 .
14. 假设要考察某公司生产的狂犬疫苗的剂量是否达标,现从500支疫苗中抽取50支进行检验,利用随机数表抽取样本时,先将500支疫苗按000,001,…,499进行编号,如果从随机数表第7行第8列的数开始向右读,请写出第3支疫苗的编号.(下面摘取了随机数表第7行至第9行)84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
15. 若随机变量ξ~N(2,1),且 ,则 =.16. 某单位200名职工的年龄分布情况如图所示,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1~200编号,并按编号顺序平均分为40组(1~5号为第1组,6~10号为第2组,…,196~200号为第40组).若第5组抽出的号码为22,则第8组抽出的号码是 .若用分层抽样方法,则40岁以下年龄段应抽取 人,则 . 17. 某校早上8∶00开始上课,假设该校学生小张与小王在早上7∶30~7∶50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为 . (用数字作答)18. 已知 ,点P的坐标为 ,则当 时,且满足 的概率为 .19. 以下四个命题,其中正确的序号是。
17. 某校早上8∶00开始上课,假设该校学生小张与小王在早上7∶30~7∶50之间到校,且每人在该时间段的任何时刻到校是等可能的,则小张比小王至少早5分钟到校的概率为 . (用数字作答)18. 已知 ,点P的坐标为 ,则当 时,且满足 的概率为 .19. 以下四个命题,其中正确的序号是。①从匀速传递的产品生产流水线上,每20分钟从中抽取一件产品进行检测,这样的抽样是分层抽样。②两个随机变量的线性相关性越强,则相关系数的绝对值越接近于1。
③在线性回归方程 中,当解释变量 每增加一个单位时,预报变量 平均增加0.2个单位。④分类变量 与 ,它们的随机变量 的观测值为 ,当 越小,“ 与 有关系”的把握程度越大。
20. 从自动打包机包装的食盐中,随机抽取20袋,测得各袋的质量分别为 单位: :492 496 494 495 498 497 501 502 504 496
497 503 506 508 507 492 496 500 501 499
根据频率分布估计总体分布的原理,该自动包装机包装的袋装食盐质量在 之间的概率约为 .
三、解答题
-
21. 城市公交车的数量太多容易造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的60名候车的乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示:
组别
一
二
三
四
五
候车时间(分钟)
人数
2
6
4
2
1
(1)、估计这15名乘客的平均候车时间;(2)、估计这60名乘客中候车时间少于10分钟的人数;(3)、若从上表第三,四组的6人中选2人作进一步的问卷调查,求抽到的2人恰好来自不同组的概率。22. 某工厂生产的某产品按照每箱10件包装,每箱产品在流入市场之前都要检验.若整箱产品检验不通过,除去检验费用外,每箱还要损失100元.检验方案如下:第一步,一次性随机抽取2件,若都合格则整箱产品检验通过;若都不合格则整箱产品检验不通过,检验结束,剩下的产品不再检验.若抽取的2件产品有且仅有1件合格,则进行第二步工作.
第二步,从剩下的8件产品中再随机抽取1件,若不合格,则整箱产品检验不通过,检验结束,剩下的产品不再检验.若合格,则进行第三步工作.
第三步,从剩下的7件产品中随机抽取1件,若不合格,则整箱产品检验不通过,若合格,则整箱产品检验通过,检验结束,剩下的产品都不再检验.
假设某箱该产品中有8件合格品,2件次品.
(Ⅰ)求该箱产品被检验通过的概率;
(Ⅱ)若每件产品的检验费用为10元,设该箱产品的检验费用和检验不通过的损失费用之和为 ,求 的分布列和数学期望 .
23. 某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示 . (1)、求毕业大学生月收入在 的频率;(2)、根据频率分别直方图算出样本数据的中位数;(3)、为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在 的这段应抽取多少人?24. 如图是某市3月1日至14日的空气质量指数趋势图 空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染 某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(1)、求毕业大学生月收入在 的频率;(2)、根据频率分别直方图算出样本数据的中位数;(3)、为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在 的这段应抽取多少人?24. 如图是某市3月1日至14日的空气质量指数趋势图 空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染 某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.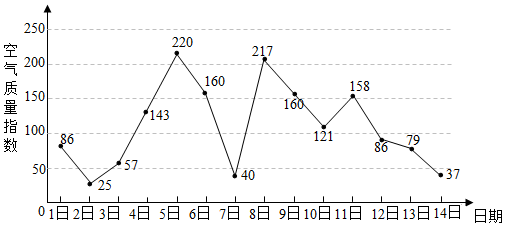
Ⅰ 求此人到达当日空气质量优良的概率;
Ⅱ 求此人在该市停留期间只有1天空气重度污染的概率;
Ⅲ 由图判断从哪天开始连续三天的空气质量指数方差最大? 结论不要求证明
25. 随着互联网的快速发展,基于互联网的共享单车应运而生,某市场研究人员为了了解共享单车运营公司 的经营状况,对该公司最近六个月的市场占有率进行了统计,并绘制了相应的折线图: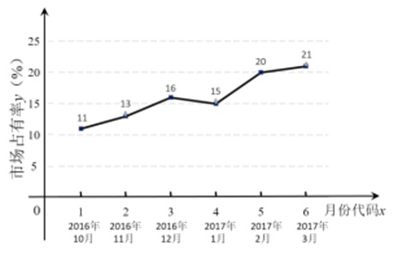
参考公式:回归直线方程为 ,其中 , .
(1)、由折线图可以看出,可用线性回归模型拟合月度市场占有率 与月份代码 之间的关系,求 关于 的线性回归方程,并预测 公司2017年4月的市场占有率;(2)、为进一步扩大市场,公司拟再采购一批单车,现有采购成本分别为 元/辆和1200元/辆的 、 两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致单车使用寿命各不相同,考虑到公司运营的经济效益,该公司决定先对这两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命的频数表如下:寿命
车型
1年
2年
3年
4年
总计
A
20
35
35
10
100
B
10
30
40
20
100
经测算,平均每辆单车每年可以带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率,如果你是 公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?