2019年高考数学二轮复习专题06:不等式与线性规划
试卷更新日期:2019-02-21 类型:二轮复习
一、单选题
-
1. 已知实数 满足条件 ,令 ,则 的最小值为( )A、
 B、
B、 C、
C、 D、
D、 2. 设x,y满足约束条件 ,若目标函数 仅在点(1,0)处取得最小值,则a的取值范围( )A、(-6,-3) B、(-6,3) C、(0,3) D、(-6,0]3. 已知 ,则z=22x+y的最小值是( )A、1 B、16 C、8 D、44. 满足线性约束条件 的目标函数 的最大值是 ( )A、1 B、 C、2 D、35. 记 为 中的最小值,若 为任意正实数,则 的最大值是( )A、 B、2 C、
2. 设x,y满足约束条件 ,若目标函数 仅在点(1,0)处取得最小值,则a的取值范围( )A、(-6,-3) B、(-6,3) C、(0,3) D、(-6,0]3. 已知 ,则z=22x+y的最小值是( )A、1 B、16 C、8 D、44. 满足线性约束条件 的目标函数 的最大值是 ( )A、1 B、 C、2 D、35. 记 为 中的最小值,若 为任意正实数,则 的最大值是( )A、 B、2 C、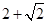 D、
6. 下列函数中,最小值为4的是( )A、
D、
6. 下列函数中,最小值为4的是( )A、 B、
B、 C、
C、 D、
D、 7. 已知实系数一元二次方程 的两个实根为 , ,且 ,则 的取值范围是( )A、
7. 已知实系数一元二次方程 的两个实根为 , ,且 ,则 的取值范围是( )A、 B、
B、 C、
C、 D、
D、 8. 设 , 若3是 与 的等比中项,则 的最小值为A、4 B、2 C、1 D、9. 若关于x的不等式 在区间 内有解,则实数a的取值范围是A、
8. 设 , 若3是 与 的等比中项,则 的最小值为A、4 B、2 C、1 D、9. 若关于x的不等式 在区间 内有解,则实数a的取值范围是A、 B、
B、 C、
C、 D、
D、 10. 设 满足约束条件 ,则 的最小值与最大值的和为( )A、7 B、8 C、13 D、1411. 若正实数 满足 ,则 的最小值为( )A、 B、
10. 设 满足约束条件 ,则 的最小值与最大值的和为( )A、7 B、8 C、13 D、1411. 若正实数 满足 ,则 的最小值为( )A、 B、 C、
D、
C、
D、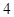 12. 已知m,n R,且m﹣2n+6=0,则 的最小值为( )A、 B、4 C、
12. 已知m,n R,且m﹣2n+6=0,则 的最小值为( )A、 B、4 C、 D、3
D、3
二、填空题
-
13. 设变量 满足约束条件 ,则 的最大值是.14. 已知 ,则函数 的取值范围是 .15. 设任意实数 ,要使 恒成立,则 的最小值为 .16. 已知 ,且 ,则 的最大值是 , 的最小值是.17. 已知变量 满足约束条件 若目标函数 的最小值为2,则 的最小值为 .