2019年高考数学二轮复习专题05:平面向量
试卷更新日期:2019-02-21 类型:二轮复习
一、单选题
-
1. 已知向量 与 的夹角为120°, 则
 ( ) A、5 B、4 C、3 D、12. 如图,在圆 中,若 , ,则 的值等于( )
( ) A、5 B、4 C、3 D、12. 如图,在圆 中,若 , ,则 的值等于( ) A、
A、 B、
B、 C、
C、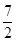 D、
3. 中,已知点 为 边上一点,若 , ,则 ( )A、
D、
3. 中,已知点 为 边上一点,若 , ,则 ( )A、 B、
B、 C、
C、 D、
D、 4. 如图,在平面四边形ABCD中, , , , . 若点E为边CD上的动点,则 的最小值为 ( )
4. 如图,在平面四边形ABCD中, , , , . 若点E为边CD上的动点,则 的最小值为 ( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 如图所示,矩形 的对角线相交于点 , 为 的中点,若 ( 、 为实数),则 ( )
5. 如图所示,矩形 的对角线相交于点 , 为 的中点,若 ( 、 为实数),则 ( )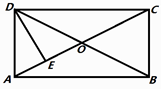 A、 B、 C、 D、6. 在 中, , ,则( )A、
A、 B、 C、 D、6. 在 中, , ,则( )A、 B、
B、 C、
C、 D、
D、 7. 若向量 , 满足 , , ,则 与 的夹角为A、
7. 若向量 , 满足 , , ,则 与 的夹角为A、 B、
B、 C、
C、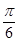 D、
D、 8. 已知平面向量 ,且 ,则 ( )A、
8. 已知平面向量 ,且 ,则 ( )A、 B、
B、 C、
C、 D、
D、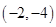 9. 已知正三角形 的边长为 ,平面 内的动点 满足 , ,则 的最大值是( )A、
9. 已知正三角形 的边长为 ,平面 内的动点 满足 , ,则 的最大值是( )A、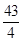 B、
B、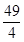 C、
C、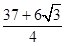 D、
D、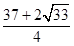 10. 已知 中, , , , 为AB边上的中点,则 ( )A、0 B、25 C、50 D、100
10. 已知 中, , , , 为AB边上的中点,则 ( )A、0 B、25 C、50 D、100二、填空题
-
11. 设向量 , 满足 , ,则 .12. 若 是夹角为 的两个单位向量, ,则 的夹角为 .13. 在△ABC中,CA=2CB=2, ,O是△ABC的外心, 若 =x +y ,则x+y= .14. 已知向量 ,若 ,则 .15. 已知向量 , 满足 , , ,则 在 上的投影的最小值是 .16. 已知 =(cosθ,sinθ), =(3-cosθ,4-sinθ),若 ∥ ,则cos2θ=.17. 定义平面向量的一种运算: ( 是向量 和 的夹角),则下列命题:
① ;② ;③若 且 ,则 ;其中真命题的序号是.
三、解答题
-
18. 已知 分别为椭圆 的左、右焦点,点 在椭圆 上.(1)、求 的最小值;(2)、若 且 ,已知直线 与椭圆 交于两点 ,过点 且平行于直线 的直线交椭圆 于另一点 ,问:四边形 能否成为平行四边形?若能,请求出直线 的方程;若不能,请说明理由.