2019年高考数学二轮复习专题03:数列
试卷更新日期:2019-02-21 类型:二轮复习
一、单选题
-
1. 我国古代数学典籍 九章算术 第七章“盈不足”中有一道两鼠穿墙问题:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何”,翻译过来就是:有五尺厚的墙,两只老鼠从墙的两边相对分别打洞穿墙,大、小鼠第一天都进一尺,以后每天,大鼠加倍,小鼠减半,则几天后两鼠相遇,这个问题体现了古代对数列问题的研究,现将墙的厚度改为1000尺,则需要几天时间才能打穿 结果取整数A、8 B、9 C、10 D、112. 公差不为0的等差数列 的前n项和为 ,若 ,且 ,则 的值为( )A、15 B、25 C、13 D、233. 已知等比数列 中, , ,则 ( )A、2 B、
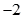 C、
C、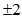 D、4
4. 已知等差数列 的公差和首项都不为 ,且 成等比数列,则 ( )A、
D、4
4. 已知等差数列 的公差和首项都不为 ,且 成等比数列,则 ( )A、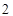 B、
C、
D、7
5. 等差数列 中 , ,则其前 项和 取最大值时 的值为( )A、503 B、504 C、503或504 D、5056. 两个等差数列 或 ,其前 项和分别为 和 ,且 ,则 ( )A、
B、
C、
D、7
5. 等差数列 中 , ,则其前 项和 取最大值时 的值为( )A、503 B、504 C、503或504 D、5056. 两个等差数列 或 ,其前 项和分别为 和 ,且 ,则 ( )A、 B、
B、 C、
C、 D、
7. 整数列 满足 ,则 ( )A、
D、
7. 整数列 满足 ,则 ( )A、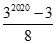 B、
B、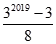 C、
C、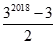 D、
D、 8. 已知数列 的前n项和为 ,且 ,则 等于A、
8. 已知数列 的前n项和为 ,且 ,则 等于A、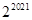 B、
B、 C、
C、 D、
D、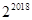 9. 已知函数 对任意实数a,b满足 ,且 ,若 ,则数列 的前9项和为A、9 B、
9. 已知函数 对任意实数a,b满足 ,且 ,若 ,则数列 的前9项和为A、9 B、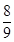 C、
C、 D、1
10. 已知{an}是公差为1的等差数列;Sn为{an}的前n项和,若S8=4S4 , 则a10=( )A、
D、1
10. 已知{an}是公差为1的等差数列;Sn为{an}的前n项和,若S8=4S4 , 则a10=( )A、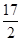 B、
B、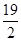 C、10
D、12
11. 已知数列 则 是它的( )A、第
C、10
D、12
11. 已知数列 则 是它的( )A、第 项
B、第
项
B、第  项
C、第 项
D、第
项
C、第 项
D、第 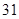 项
12. 等差数列{an}中,a1+a5=14,a4=10,则数列{an}的公差为( )A、1 B、2 C、3 D、413. 设等差数列{an}的公差为d , 若数列{2a1an}为递减数列,则 ( )
项
12. 等差数列{an}中,a1+a5=14,a4=10,则数列{an}的公差为( )A、1 B、2 C、3 D、413. 设等差数列{an}的公差为d , 若数列{2a1an}为递减数列,则 ( )
A、d<0 B、d>0 C、a1d<0 D、a1d>0二、填空题
-
14. 已知等差数列 的公差 ,且 成等比数列,若 为数列 的前 项和,则 的最小值为.15. 已知数列 为等差数列,其前 项和为 ,且 ,给出以下结论:① ② 最小③ ④ ,正确的有.16. 数列 中, 且 ,则17. 在各项均为正数的等比数列 中,若 ,则 .18. 已知等比数列 , , 的公比分别为2,A,B记 , , ,则 .19. 数列 且 ,若 为数列 的前n项和,则 .
三、解答题
-
20. 已知数列 满足 , ( ).
(Ⅰ)证明数列 为等差数列,并求 的通项公式;
(Ⅱ)设数列 的前 项和为 ,若数列 满足 ,且 对任意的 恒成立,求 的最小值.
21. 已知数列 的前n项和为 , ,且(1)、求数列 的通项公式;(2)、设 ,求 的前n项和 .22. 已知数列 满足 ( , ),且 , .(1)、证明:数列 是等比数列;(2)、求数列 的前 项和 .