2019年高考数学二轮复习专题01:集合与常用逻辑用语
试卷更新日期:2019-02-21 类型:二轮复习
一、单选题
-
1. 已知集合 , ,则 ( )A、
 B、
B、 C、
C、 D、
D、 2. 已知集合A= ,B= ,则 =( )A、
2. 已知集合A= ,B= ,则 =( )A、 B、
B、 C、
C、 D、
D、 3. 设全集为R,函数 的定义域为M,则 为 ( )A、(-∞,1) B、(1,+∞) C、(-∞,1] D、[1,+∞)4. 已知集合 , ,则 ( )A、
3. 设全集为R,函数 的定义域为M,则 为 ( )A、(-∞,1) B、(1,+∞) C、(-∞,1] D、[1,+∞)4. 已知集合 , ,则 ( )A、 B、
B、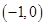 C、
C、 D、
D、 5. 若集合 , ,则( )A、
5. 若集合 , ,则( )A、 B、
B、 C、
C、 D、
D、 6. 如图所示, 是全集, 是 的子集,则阴影部分所表示的集合是( )
6. 如图所示, 是全集, 是 的子集,则阴影部分所表示的集合是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 若非空集合 , , 满足 ,且 不是 的子集, 则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件8. 命题:“ ,使 ”,这个命题的否定是A、
7. 若非空集合 , , 满足 ,且 不是 的子集, 则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件8. 命题:“ ,使 ”,这个命题的否定是A、 ,使
,使  B、
B、 ,使
,使  C、
C、 ,使
,使  D、
D、 ,使
,使  9. 已知命题p:命题“ ”的否定是“ ”;命题q:在△ABC中角A、B、C的对边分别为a、b、c,则“ ”是“a>b”的充要条件,则下列命题为真命题的是( )A、
9. 已知命题p:命题“ ”的否定是“ ”;命题q:在△ABC中角A、B、C的对边分别为a、b、c,则“ ”是“a>b”的充要条件,则下列命题为真命题的是( )A、 B、
B、 C、
C、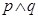 D、
D、 10. 已知 .若“ ”是真命题,则实数a的取值范围是( )A、(1,+∞) B、(-∞,3) C、(1,3) D、
10. 已知 .若“ ”是真命题,则实数a的取值范围是( )A、(1,+∞) B、(-∞,3) C、(1,3) D、 11. 已知 , , , ,则 是 ( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件12. 已知命题 : , ,则命题 的否定为( )A、
11. 已知 , , , ,则 是 ( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件12. 已知命题 : , ,则命题 的否定为( )A、 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  13. 下列说法正确的是( )A、命题“
13. 下列说法正确的是( )A、命题“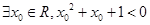 ”的否定是:“
”的否定是:“ 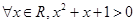 ”
B、“
”
B、“ 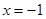 ”是“
”是“ 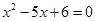 ”的必要不充分条件
C、命题“若
”的必要不充分条件
C、命题“若 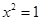 ,则 ”的否命题是:若
,则 ”的否命题是:若 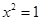 ,则
,则 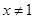 D、命题“若 ,则
D、命题“若 ,则 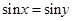 ”的逆否命题为真命题.
14. 有下列四个命题:
”的逆否命题为真命题.
14. 有下列四个命题:⑴“若 ,则 , 互为倒数”的逆命题;(2)“面积相等的三角形全等”的否命题;(3)“若 ,则 有实数解”的逆否命题;(4)“若 ,则 ”的逆否命题.其中真命题为( )
A、(1)(2) B、(2)(3) C、(4) D、(1)(2)(3)二、填空题
-
15. 已知 , , ,则 , .16. 条件 ,条件 ,若 是 的充分不必要条件,则实数 的取值范围是 .17. 已知命题p:对任意的 ,不等式 恒成立,则 为;若 为假命题,则m的取值范围是 .
三、解答题
-
18. 设全集 .(1)、当 时,求 ;(2)、若 ,求实数 的取值范围.