河北省省级示范高中联合体2018-2019学年高三上学期理数12月联考试卷
试卷更新日期:2019-02-20 类型:高考模拟
一、单选题
-
1. 若 ,则 ( )A、 B、
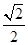 C、1
D、
2. 设集合 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 曲线 在点 处的切线的斜率为( )A、0 B、1 C、2 D、4. 设等比数列 的前 项和为 ,且 ,则 ( )A、4 B、 C、 D、
C、1
D、
2. 设集合 , ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 曲线 在点 处的切线的斜率为( )A、0 B、1 C、2 D、4. 设等比数列 的前 项和为 ,且 ,则 ( )A、4 B、 C、 D、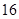 5. 如图,在 中 , , 是 边上的高.若从 内部随机取一点,则此点取自阴影部分的概率为( )
5. 如图,在 中 , , 是 边上的高.若从 内部随机取一点,则此点取自阴影部分的概率为( ) A、 B、 C、 D、6. 设 , 满足约束条件 ,则 的取值范围为( )A、
A、 B、 C、 D、6. 设 , 满足约束条件 ,则 的取值范围为( )A、 B、
B、 C、
C、 D、
D、 7. 展开式中 的系数为( )A、1 B、-9 C、31 D、-198. 三棱锥 的三视图如图所示, , , , 在三视图中所对应的点分别为 , , , ,则 与平面 所成角的正切值为( )
7. 展开式中 的系数为( )A、1 B、-9 C、31 D、-198. 三棱锥 的三视图如图所示, , , , 在三视图中所对应的点分别为 , , , ,则 与平面 所成角的正切值为( ) A、 B、 C、2 D、9. 已知点 为双曲线 的右顶点,过 的直线 与 的两条渐近线分别交于 , 两点.若 , 分别在第一、第四象限内,且 ,则 的方程为( )A、
A、 B、 C、2 D、9. 已知点 为双曲线 的右顶点,过 的直线 与 的两条渐近线分别交于 , 两点.若 , 分别在第一、第四象限内,且 ,则 的方程为( )A、 B、
B、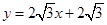 C、
C、 D、
D、 10. 设 , ,则 ( )A、
10. 设 , ,则 ( )A、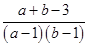 B、
B、 C、
C、 D、
D、 11. 已知椭圆 的右焦点为 , 为 上的动点, ,若 的周长的最大值为 ,则 的离心率为( )A、
11. 已知椭圆 的右焦点为 , 为 上的动点, ,若 的周长的最大值为 ,则 的离心率为( )A、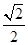 B、
C、
D、
12. 设正三棱锥 的每个顶点都在半径为2的球 的球面上,则三棱锥 体积的最大值为( )A、
B、
C、
D、
12. 设正三棱锥 的每个顶点都在半径为2的球 的球面上,则三棱锥 体积的最大值为( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 已知向量 , 的夹角为 ,且 ,则 .14. 若函数 ,在 上是单调函数,则 的取值范围为 .15. 设数列 的通项公式为 , 为其前 项和,则数列 的前9项和 .16. 已知函数 在 上单调,且 ,则正数 的值为 .
三、解答题
-
17. 的内角 , , 的对边分别为 , , ,且 .(1)、求 ;(2)、若 ,求 .18. 如图,四边形 为正方形, ,且 , 平面 .
 (1)、证明:平面 平面 ;(2)、求二面角 的余弦值.19. 某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:
(1)、证明:平面 平面 ;(2)、求二面角 的余弦值.19. 某工厂共有男女员工500人,现从中抽取100位员工对他们每月完成合格产品的件数统计如下:每月完成合格产品的件数(单位:百件)
频数
10
45
35
6
4
男员工人数
7
23
18
1
1
附: ,
 .(1)、其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?
.(1)、其中每月完成合格产品的件数不少于3200件的员工被评为“生产能手”.由以上统计数据填写下面 列联表,并判断是否有95%的把握认为“生产能手”与性别有关?非“生产能手”
“生产能手”
合计
男员工
女员工
合计
(2)、为提高员工劳动的积极性,工厂实行累进计件工资制:规定每月完成合格产品的件数在定额2600件以内的,计件单价为1元;超出 件的部分,累进计件单价为1.2元;超出 件的部分,累进计件单价为1.3元;超出400件以上的部分,累进计件单价为1.4元.将这4段中各段的频率视为相应的概率,在该厂男员工中选取1人,女员工中随机选取2人进行工资调查,设实得计件工资(实得计件工资=定额计件工资+超定额计件工资)不少于3100元的人数为,求的分布列和数学期望.20. 已知抛物线 ,点 为 的焦点,过 的直线 交 于 , 两点.(1)、设 , 在 的准线上的射影分别为 , ,线段 的中点为 ,证明: .(2)、在 轴上是否存在一点 ,使得直线 , 的斜率之和为定值?若存在,求出点 的坐标;若不存在,请说明理由.