浙江省嘉兴市2016-2017学年下学期期中联考八年级数学学科试题卷
试卷更新日期:2017-04-18 类型:期中考试
一、选择题.
-
1. 化简
 的结果是( )
的结果是( )
A、3 B、 C、±3 D、92. 下列计算中正确的是( )A、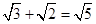 B、
B、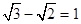 C、
C、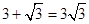 D、
D、 3.
3.用配方法解一元二次方程
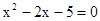 时,可配方得( )A、
时,可配方得( )A、 B、
B、 C、
C、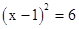 D、
D、 4. 已知x=2是方程
4. 已知x=2是方程 的一个解,则
的一个解,则  的值是( ) A、3 B、4 C、5 D、65. 有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )A、10 B、 C、 D、26.
的值是( ) A、3 B、4 C、5 D、65. 有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )A、10 B、 C、 D、26.如图,在平行四边形ABCD中,∠B=60度,AB=5cm,则下面结论正确的是( )
 A、BC=5cm,∠D=60度 B、∠C=120度,CD=5cm C、AD=5cm,∠A=60度 D、∠A=120度,AD=5cm7. 若n边形的内角和等于外角和的2倍,则边数n为( )A、 n=4 B、n=5 C、n=6 D、n=78. 已知 ,则化简 的结果是( )
A、BC=5cm,∠D=60度 B、∠C=120度,CD=5cm C、AD=5cm,∠A=60度 D、∠A=120度,AD=5cm7. 若n边形的内角和等于外角和的2倍,则边数n为( )A、 n=4 B、n=5 C、n=6 D、n=78. 已知 ,则化简 的结果是( )
A、4 B、 C、 D、9.在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2 , 设金色纸边的宽为xcm,那么x满足的方程(化为一般形式)是( )
 A、
A、 B、
B、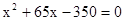 C、
C、 D、
D、 10. 如果一元二次方程 满足 ,那么我们称这个方程为“阿凡达”方程,已知 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
10. 如果一元二次方程 满足 ,那么我们称这个方程为“阿凡达”方程,已知 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A、 B、 C、 D、二、填空题。
-
11. 当 =-2时,则二次根式 的值为 .12. 请写出一个与 的积为有理数的数是 .13. 四边形ABCD中,∠A与∠C互补,∠B=80°,则∠D=度.
14. 如图,斜坡AC的坡比为0.8:1,若BC=5,则斜坡AC= . 15. 随着经济的发展,桐乡房价从2015年的8000元/平方米,增长到2017年的11520元/平方米,设平均每年的增长率相同为x,则根据题意可列方程为.16. 某中学随机调查了15名学生,了解他们一周在校参加体育锻炼时间,列表如下:
15. 随着经济的发展,桐乡房价从2015年的8000元/平方米,增长到2017年的11520元/平方米,设平均每年的增长率相同为x,则根据题意可列方程为.16. 某中学随机调查了15名学生,了解他们一周在校参加体育锻炼时间,列表如下:锻炼时间(小时)
5
6
7
8
人数
2
6
5
2
则这15名同学一周在校参加体育锻炼时间的中位数和众数分别是 .
17. 如图,AC、BD是平行四边形ABCD的对角线,AC与BD交于点O,AC=4,BD=5,BC=3,则△BOC的周长是 . 18. 已知 的整数部分是 ,小数部分是 ,则 .
18. 已知 的整数部分是 ,小数部分是 ,则 .
19. 若关于 的一元二次方程 有实数根,则m的取值范围是 .
20. 为迎接G20杭州峰会的召开,某校八年级(1)(2)班准备集体购买一种T恤衫参加一项社会活动.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.如果八(1)(2)班共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买数量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,则第一批T恤衫的购买件.
三、解答题:
-
21. 解答题。(1)、计算:(2)、
22. 请选择适当的方法解下列一元二次方程:(1)、(2)、23. 小明和小聪最近5次数学测试的成绩如下:小聪:76 84 80 87 73
小明:78 82 79 80 81
(1)、分别求出小明和小聪的平均成绩;(2)、哪位同学的数学成绩比较稳定.
24.已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。

求证:
(1)、△ADF≌△CBE(2)、EB∥DF.25.如图,某公司计划用32m长的材料沿墙建造的长方形仓库,仓库的一边靠墙,已知墙长16m,设长方形的宽AB为xm.
 (1)、用x的代数式表示长方形的长BC;(2)、能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;(3)、能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
(1)、用x的代数式表示长方形的长BC;(2)、能否建造成面积为120㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由;(3)、能否建造成面积为160㎡的长方形仓库?若能,求出长方形仓库的长和宽;若不能,请说明理由.
26. 如图,在Rt△ABC中,∠B=90°,直角边AB、BC的长(AB<BC)是方程 2-7 +12=0的两个根.点P从点A出发,以每秒1个单位的速度沿△ABC边 A→B→C→A的方向运动,运动时间为t(秒). (1)、求AB与BC的长;(2)、当点P运动到边BC上时,试求出使AP长为 时运动时间t的值;(3)、点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.
(1)、求AB与BC的长;(2)、当点P运动到边BC上时,试求出使AP长为 时运动时间t的值;(3)、点P在运动的过程中,是否存在点P,使△ABP是等腰三角形?若存在,请求出运动时间t的值;若不存在,请说明理由.