2017年湖北省宜昌市枝江市中考数学模拟试卷(3月份)
试卷更新日期:2017-04-18 类型:中考模拟
一、选择题
-
1. ﹣ 的相反数是( )A、﹣3 B、 C、3 D、﹣2. 在一些汉字的美术字中,有的是轴对称图形.下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有 个.( )
A、2个 B、3个 C、4个 D、5个3. 下列计算正确的是( )A、2a•3a=6a B、(﹣a3)2=a6 C、6a÷2a=3a D、(﹣2a)3=﹣6a34. 在践行社会主义核心价值观活动中,共评选出各级各类“湖北好人”45 000多名.45 000这个数用科学记数法表示为( )A、4.5×103 B、4.5×104 C、4.5×105 D、0.45×1055. 若 ,则用只含x的代数式表示为( )A、y=2x+7 B、y=7﹣2x C、y=﹣2x﹣5 D、y=2x﹣56. 下列一元二次方程中,有两个不相等实数根的方程是( )A、x2﹣3x+1=0 B、x2+1=0 C、x2﹣2x+1=0 D、x2+2x+3=07. 不等式组 的解集在数轴上表示正确的是( )A、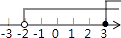 B、
B、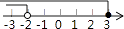 C、
C、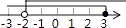 D、
D、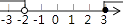 8. 下列说法:
8. 下列说法:①36的平方根是6; ②±9的平方根是±3; ③ =±4; ④0.01是0.1的平方根; ⑤42的平方根是4; ⑥81的算术平方根是±9.
其中正确的说法是( )
A、0 B、1 C、3 D、59. 将一副三角板如图放置,使点A在DE上,BC∥DE,则∠AFC的度数为( ) A、45° B、50° C、60° D、75°10. 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则 的长为( )
A、45° B、50° C、60° D、75°10. 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则 的长为( ) A、 π B、π C、 D、11. 某工厂现在平均每天比原计划多生产50台机器,现在生产800台所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 = B、 = C、 = D、 =12. 九(2)班体育委员用划记法统计本班40名同学投掷实心球的成绩,结果如图所示:则这40名同学投掷实心球的成绩的众数和中位数分别是( )
A、 π B、π C、 D、11. 某工厂现在平均每天比原计划多生产50台机器,现在生产800台所需时间与原计划生产600台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是( )A、 = B、 = C、 = D、 =12. 九(2)班体育委员用划记法统计本班40名同学投掷实心球的成绩,结果如图所示:则这40名同学投掷实心球的成绩的众数和中位数分别是( )成绩
6
7
8
9
10
人数
正
一
正
正
一
正
正

正
A、8,8 B、8,8.5 C、9,8 D、9,8.513. 同时抛掷A,B两个均匀的小正方体(每个面上分别标有数字1、2、3、4、5、6),设两个正方体朝上的数字分别是x,y,并以此确定点P(x,y),那么点P落在抛物线y=﹣x2+3x上的概率是( )A、 B、 C、 D、14.如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )
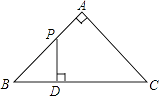 A、
A、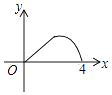 B、
B、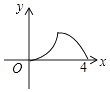 C、
C、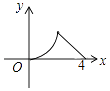 D、
D、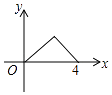
二、解答题
-
15. 计算: +|1﹣ |+ +( )﹣1﹣20170 .16. 化简: ,然后在不等式x≤2的非负整数解中选择一个适当的数代入求值.17. 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
 (1)、求证:AB=AC;(2)、若AD=2 ,∠DAC=30°,求AC的长.18. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1= (x<0)图象上一点,AO的延长线交函数y2= (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC= ,求函数y2 .
(1)、求证:AB=AC;(2)、若AD=2 ,∠DAC=30°,求AC的长.18. 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y1= (x<0)图象上一点,AO的延长线交函数y2= (x>0,k<0)的y2图象于点B,BC⊥x轴,若S△ABC= ,求函数y2 . 19. 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下表:
19. 在某项针对18~35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当m≥10时为A级,当5≤m<10时为B级,当0≤m<5时为C级.现随机抽取30个符合年龄条件的青年人开展每人“日均发微博条数”的调查,所抽青年人的“日均发微博条数”的数据如下表:11
10
6
15
9
16
13
12
0
8
2
8
10
17
6
13
7
5
7
3
12
10
7
11
3
6
8
14
15
12
(1)、求样本数据中为A级的频率;(2)、试估计1000个18~35岁的青年人中“日均发微博条数”为A级的人数;(3)、从样本数据为C级的人中随机抽取2人,用列举法求抽得2个人的“日均发微博条数”都是3的概率.20. 如图A、F、B、C是半圆O上的四个点,四边形OABC是平行四边形,∠FAB=15°,连接OF交AB于点E,过点C作OF的平行线交AB的延长线于点D,延长AF交直线CD于点H. (1)、求证:CD是半圆O的切线;(2)、求 的比值;若DH=6,求EF和半径OA的长.21. 青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.(1)、请问每个站点的造价和公共自行车的单价分别是多少万元?(2)、请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.22.
(1)、求证:CD是半圆O的切线;(2)、求 的比值;若DH=6,求EF和半径OA的长.21. 青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.(1)、请问每个站点的造价和公共自行车的单价分别是多少万元?(2)、请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.22.如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
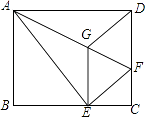 (1)、求证:四边形EFDG是菱形;(2)、探究线段EG、GF、AF之间的数量关系,并说明理由;(3)、若AG=6,EG=2 ,求BE的长.23.
(1)、求证:四边形EFDG是菱形;(2)、探究线段EG、GF、AF之间的数量关系,并说明理由;(3)、若AG=6,EG=2 ,求BE的长.23.如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
 (1)、求经过A、B、C三点的抛物线的解析式;(2)、当BE经过(1)中抛物线的顶点时,求CF的长;(3)、连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
(1)、求经过A、B、C三点的抛物线的解析式;(2)、当BE经过(1)中抛物线的顶点时,求CF的长;(3)、连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.