2017年湖北省孝感市中考数学一模试卷
试卷更新日期:2017-04-18 类型:中考模拟
一、选择题
-
1. 下列四个数中,正整数是( )A、﹣2 B、﹣1 C、0 D、12. 下列等式一定成立的是( )A、2a+3b=5ab B、(a3)2=a5 C、a2•a3=a5 D、(a+b)2=a2+b23.
2017年某市获“全国文明城市”提名,为此小王特制了一个正方体玩具,其展开图如图所示,正方体中与“全”字对面的字是( )
 A、文 B、明 C、城 D、市4. 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A、文 B、明 C、城 D、市4. 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( ) A、30° B、40° C、50° D、60°5. 点M(cos30°,sin30°)关于原点中心对称的点的坐标是( )A、( , ) B、(﹣ ,﹣ ) C、(﹣ , ) D、(﹣ ,﹣ )6.
A、30° B、40° C、50° D、60°5. 点M(cos30°,sin30°)关于原点中心对称的点的坐标是( )A、( , ) B、(﹣ ,﹣ ) C、(﹣ , ) D、(﹣ ,﹣ )6.如图,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动.设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )
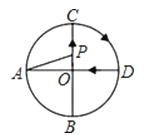 A、
A、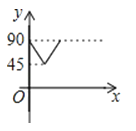 B、
B、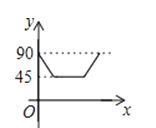 C、
C、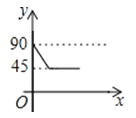 D、
D、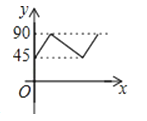 7. 如图,已知点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( )
7. 如图,已知点E(﹣4,2),F(﹣2,﹣2),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为( ) A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,﹣4) C、(2,﹣1) D、(8,﹣4)8. 已知二次函数y=ax2﹣bx+c(a≠0),其图象经过A(3﹣m,2),B(m+1,2)两点,则 的值为( )A、2 B、﹣2 C、4 D、﹣49. 如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( )
A、(2,﹣1)或(﹣2,1) B、(8,﹣4)或(﹣8,﹣4) C、(2,﹣1) D、(8,﹣4)8. 已知二次函数y=ax2﹣bx+c(a≠0),其图象经过A(3﹣m,2),B(m+1,2)两点,则 的值为( )A、2 B、﹣2 C、4 D、﹣49. 如图,正方形ABCD的四个顶点在坐标轴上,A点坐标为(3,0),假设有甲、乙两个物体分别由点A同时出发,沿正方形ABCD的边作环绕运动,物体甲按逆时针方向匀速运动,物体乙按顺时针方向匀速运动,如果甲物体12秒钟可环绕一周回到A点,乙物体24秒钟可环绕一周回到A点,则两个物体运动后的第2017次相遇地点的坐标是( ) A、(3,0) B、(﹣1,2) C、(﹣3,0) D、(﹣1,﹣2)
A、(3,0) B、(﹣1,2) C、(﹣3,0) D、(﹣1,﹣2)二、填空题
-
10. 地球与月球的距离大约为384000km,用科学记数法表示为 km.11. 在函数y= 中,自变量x的取值范围是 .12. 如图,AC是正五边形ABCDE的一条对角线,则∠ACB= .
 13. 有四张背面相同的纸牌A,B,C,D,其正面分别画有等边三角形,圆,平行四边形和正五边形,小明将这四张纸牌背面朝上洗匀后随机摸出一张,则摸出的图形是中心对称图形的概率是 .14. 已知函数y= ,其图象如图中的实线部分,图象上两个最高点分别是A,B,连接AB,则图中曲四边形ABCO(阴影部分)的面积是 .
13. 有四张背面相同的纸牌A,B,C,D,其正面分别画有等边三角形,圆,平行四边形和正五边形,小明将这四张纸牌背面朝上洗匀后随机摸出一张,则摸出的图形是中心对称图形的概率是 .14. 已知函数y= ,其图象如图中的实线部分,图象上两个最高点分别是A,B,连接AB,则图中曲四边形ABCO(阴影部分)的面积是 . 15. 如图,平面直角坐标系中,已知A点坐标(0,1),反比例函数y= (k>0,x>0)的图象与直线y=x相交于点B,P是x轴的动点,如果PA+PB的最小值是5,那么k的值是 .
15. 如图,平面直角坐标系中,已知A点坐标(0,1),反比例函数y= (k>0,x>0)的图象与直线y=x相交于点B,P是x轴的动点,如果PA+PB的最小值是5,那么k的值是 .
三、解答题
-
16. 计算下列各题(1)、计算:(﹣2)2﹣ (1+tan45°)(2)、先化简,再求值: ,其中a= ﹣2,b= +2.17. 解不等式组 .18. 为了了解市民“获取新闻的最主要途径”某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
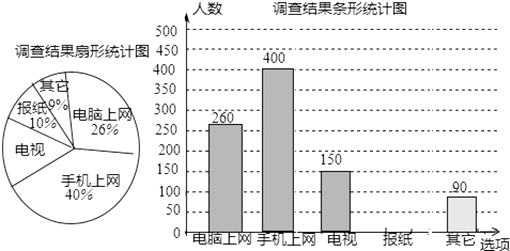
根据以上信息解答下列问题:
(1)、这次接受调查的市民总人数是;(2)、扇形统计图中,“电视”所对应的圆心角的度数是;(3)、请补全条形统计图;(4)、若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.19. 如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将▱ABCO绕点A逆时针旋转60°,得到对应的▱ADEF,解答下列问题: (1)、画出旋转后的▱ADEF(不写作法,不证明,保留作图痕迹);(2)、求▱ABCO旋转过程中扫过的区域的面积.20. 某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
(1)、画出旋转后的▱ADEF(不写作法,不证明,保留作图痕迹);(2)、求▱ABCO旋转过程中扫过的区域的面积.20. 某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:第1个
第2个
第3个
第4个
…
第n个
调整前的单价x(元)
x1
x2=6
x3=72
x4
…
xn
调整后的单价y(元)
y1
y2=4
y3=59
y4
…
yn
已知这n个玩具调整后的单价都大于2元.
(1)、求y与x的函数关系式,并确定x的取值范围;(2)、某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?(3)、这n个玩具调整前、后的平均单价分别为 , ,猜想 与 的关系式,并写出推导过程.21. 如图,已知四边形ABCD是矩形,对角线AC的垂直平分线交AD于点E,交BC于点F,连接AF,CE,解答下列问题: (1)、求证:四边形AECF是菱形;(2)、记AB=a,BF=b,若a,b是方程x2﹣2(m+1)x+m2+1=0的两根,问当m为何值时,菱形AECF的周长为8 .22. 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题:
(1)、求证:四边形AECF是菱形;(2)、记AB=a,BF=b,若a,b是方程x2﹣2(m+1)x+m2+1=0的两根,问当m为何值时,菱形AECF的周长为8 .22. 已知等边△ABC,M是边BC延长线上一点,连接AM交△ABC的外接圆于点D,延长BD至N,使得BN=AM,连接CN,MN,解答下列问题: (1)、猜想△CMN的形状,并证明你的结论;(2)、请你证明CN是⊙O的切线;(3)、若等边△ABC的边长是2,求AD•AM的值.23. 如图1,平面直角坐标系中,矩形ABCD关于y轴对称,点A,D在x轴上,BC交y轴于点F,E是OF的中点,抛物线y=ax2+bx+c经过B,E,C三点,已知点B(﹣2,﹣2),解答下列问题:
(1)、猜想△CMN的形状,并证明你的结论;(2)、请你证明CN是⊙O的切线;(3)、若等边△ABC的边长是2,求AD•AM的值.23. 如图1,平面直角坐标系中,矩形ABCD关于y轴对称,点A,D在x轴上,BC交y轴于点F,E是OF的中点,抛物线y=ax2+bx+c经过B,E,C三点,已知点B(﹣2,﹣2),解答下列问题: (1)、填空:a= , b= , c= .(2)、如图2,这P是上述抛物线上一点,连接PF并延长交抛物线于另外一点Q,PM⊥x轴于M,QN⊥x轴于N.
(1)、填空:a= , b= , c= .(2)、如图2,这P是上述抛物线上一点,连接PF并延长交抛物线于另外一点Q,PM⊥x轴于M,QN⊥x轴于N.①求证:PM+QN=PQ;
②若PQ=m,S四边形PMNQ= m2 , 求直线PQ对应的一次函数的解析式.