2017年湖北省咸宁市赤壁市中考数学一模试卷
试卷更新日期：2017-04-18 类型：中考模拟
一、精心选一选
-
1. 计算1﹣（﹣2）的正确结果是（ ）A、﹣2 B、﹣1 C、1 D、32. 钓鱼岛是中国的固有领土，面积约4400000平方米，数据4400000用科学记数法表示应为（ ）A、44×105 B、0.44×107 C、4.4×106 D、4.4×1053. 下列式子中，属于最简二次根式的是（ ）A、 B、 C、 D、4. 下列运算正确的是（ ）A、（a2）3=a5 B、a3•a=a4 C、（3ab）2=6a2b2 D、a6÷a3=a25. 下列说法中，正确的是（ ）A、“打开电视，正在播放新闻联播节目”是必然事件 B、某种彩票中奖概率为10%是指买10张一定有一张中奖 C、了解某种节能灯的使用寿命应采用全面检查 D、一组数据3，5，4，6，7的中位数是5，方差是26. 如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM．若∠AOC=70°，则∠CON的度数为（ ）
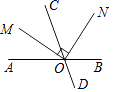A、65° B、55° C、45° D、35°7. 如图是某几何体的三视图，这个几何体的侧面积是（ ）
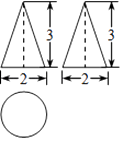A、6π B、2 π C、 π D、3π8.如图，直线l：y= x，过点A（0，1）作y轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1 ， 过点B1作直线l的垂线交y轴于点A2；…按此作法继续下去，则点A2015的坐标为（ ）
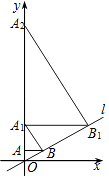A、（0，42015） B、（0，42014） C、（0，32015） D、（0，32014）二、细心填一填
-
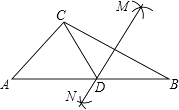
9. 分解因式：ax2﹣9ay2= ．10. 如图，在△ABC中，按以下步骤作图：
①分别以B，C为圆心，以大于 BC的长为半径作弧，两弧相交于M，N两点；
②作直线MN交AB于点D，连接CD，若CD=AC，∠B=25°，则∠ACB的度数为 ．
11. 若关于x的方程kx2+（k+2）x+ =0有两个不相等的实数根，则k的取值范围是 ．12. 如图，在△ABC中，AB=AC=5，BC=6，将△ABC绕点C顺时针方向旋转一定角度后得到△A′B′C．若点A′恰好落在BC的延长线上，则点B′到BA′的距离为 ．
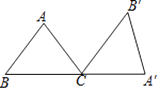13. 一辆汽车开往距离出发地180km的目的地，出发后第一小时按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，结果比原计划提前40min到达目的地．原计划的行驶速度是 km/h．14. 如图，直线AB与半径为2的⊙O相切于点C，D是⊙O上一点，且∠EDC=30°，弦EF∥AB，则EF的长度为 ．
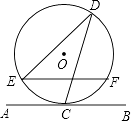15. 如图，矩形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为 ．
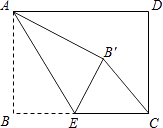16. 对于二次函数y=x2﹣2mx﹣3，有下列结论：①它的图象与x轴有两个交点；
②如果当x≤﹣1时，y随x的增大而减小，则m=﹣1；
③如果将它的图象向左平移3个单位后过原点，则m=1；
④如果当x=2时的函数值与x=8时的函数值相等，则m=5．
其中一定正确的结论是 ． （把你认为正确结论的序号都填上）
三、专心解一解
-
17. 计算下列各题(1)、计算：4sin60°﹣|3﹣ |+（ ）﹣2；(2)、解方程：x2﹣ x﹣ =0．18. 如图，点B（3，3）在双曲线y= （x＞0）上，点D在双曲线y=﹣ （x＜0）上，点A和点C分别在x轴，y轴的正半轴上，且点A，B，C，D构成的四边形为正方形．
(1)、求k的值；(2)、求点A的坐标．19. 如图，在▱ABCD中，F是AD的中点，延长BC到点E，使CE= BC，连接DE，CF．
(1)、求证：DE=CF；(2)、若AB=4，AD=6，∠B=60°，求DE的长．20. 某学校“体育课外活动兴趣小组”，开设了以下体育课外活动项目：A．足球 B．乒乓球C．羽毛球 D．篮球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：(1)、这次被调查的学生共有人，在扇形统计图中“D”对应的圆心角的度数为；(2)、请你将条形统计图补充完整；(3)、在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加市里组织的乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状图或列表法解答）．
21. 如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．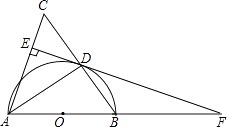
(1)、求证：EF是⊙0的切线．(2)、如果⊙0的半径为5，sin∠ADE= ，求BF的长．22. 某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．(1)、求每台A型电脑和B型电脑的销售利润；(2)、该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
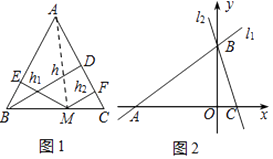
(3)、实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．23.阅读理解：运用“同一图形的面积相等”可以证明一些含有线段的等式成立，这种解决问题的方法我们称之为面积法．如图1，在等腰△ABC中，AB=AC，AC边上的高为h，点M为底边BC上的任意一点，点M到腰AB、AC的距离分别为h1、h2 ， 连接AM，利用S△ABC=S△ABM+S△ACM ， 可以得出结论：h=h1+h2 ．
类比探究：在图1中，当点M在BC的延长线上时，猜想h、h1、h2之间的数量关系并证明你的结论．
拓展应用：如图2，在平面直角坐标系中，有两条直线l1：y= x+3，l2：y=﹣3x+3，
若l2上一点M到l1的距离是1，试运用“阅读理解”和“类比探究”中获得的结论，求出点M的坐标．
24.如图，在平面直角坐标系中，已知矩形ABCD的三个顶点A（﹣3，4）、B（﹣3，0）、C（﹣1，0）．以D为顶点的抛物线y=ax2+bx+c过点B．动点P从点D出发，沿DC边向点C运动，同时动点Q从点B出发，沿BA边向点A运动，点P、Q运动的速度均为每秒1个单位，运动的时间为t秒．过点P作PE⊥CD交BD于点E，过点E作EF⊥AD于点F，交抛物线于点G．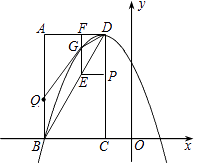
(1)、求抛物线的解析式；(2)、当t为何值时，四边形BDGQ的面积最大？最大值为多少？(3)、动点P、Q运动过程中，在矩形ABCD内（包括其边界）是否存在点H，使以B，Q，E，H为顶点的四边形是菱形，若存在，请直接写出此时菱形的周长；若不存在，请说明理由．