浙江省嘉兴市2016-2017学年下学期期中联考七年级数学学科试题卷
试卷更新日期:2017-04-18 类型:期中考试
一、选择题.
-
1. 将如图所示的图案通过平移后可以得到的图案是( )
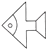 A、
A、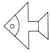 B、
B、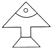 C、
C、 D、
D、 2. 下列各式中,属于二元一次方程的是( )
2. 下列各式中,属于二元一次方程的是( )
A、+y=0 B、 C、x + y 3 - 2 y = 1 1 2 3. 下列等式中成立的是( )A、a4•a=a4 B、a6﹣a3=a3 C、(ab2)3=a3•b5 D、(a3)2=a64. 方程组{ x − y = 1 2 x + y = 5
A、{ x = − 1 y = 2 { x = 2 y = − 1 { x = 2 y = 1 { x = 1 y = 2 5. 下列多项式的乘法中,能用平方差公式计算的是( )A、(-m +n)(m - n) B、(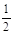 a +b)(b -
a +b)(b - 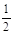 a)
C、(x + 5)(x + 5)
D、(3a-4b)(3b +4a)
6.
a)
C、(x + 5)(x + 5)
D、(3a-4b)(3b +4a)
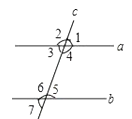
6.如图,直线a , b被直线c所截,现给出下列四个条件:
①∠1=∠5;②∠4=∠7;③∠2+∠3=180°;④∠3=∠5;
其中能判定a∥b的条件的序号是( )
 A、①② B、①③ C、①④ D、③④7. 已知
A、①② B、①③ C、①④ D、③④7. 已知m + n = 2 , m n = − 2 , ( 2 − m ) ( 2 − n )
A、2 B、-2 C、0 D、38. 如果(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A、﹣3 B、3 C、0 D、19. 《九章算术》是我国东汉初年编订的一部数学经典著作。在它的“方程”一章里,一次方程组是由算筹布置而成的,《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2,图中各行从左到右列出的算筹数分别表示未知数x , y的系数与相应的常数项,把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是:{ 3 x + 2 y = 19 x + 4 y = 23 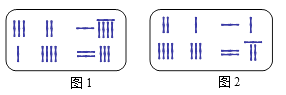 A、
A、{ 2 x + y = 11 4 x + 3 y = 27 { 2 x + y = 11 4 x + 3 y = 22 { 3 x + 2 y = 19 x + 4 y = 23 { 2 x + y = 6 4 x + 3 y = 27 10. 若∠α与∠β的两边分别平行,且∠α=(2x+10)°,∠β=(3x﹣20)°,则∠α的度数为( )A、70° B、86° C、70°或86° D、30°或38°二、填空题.
-
11. 用科学记数法表示:-0.0000419= .12. 在二元一次方程x+3y=8的解中,当x=2时,对应的y的值是 .
13. 已知四个数:3-2 , -32 , 30 , (-3)3其中最大的数是 .
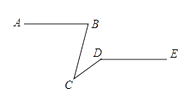
14. 写一个解为{ x = 2 y = − 1 15.如图,已知AB∥DE , ∠ABC=75°,∠CDE=150°,则∠BCD的度数为 .
 16.
16.如图是一块长方形ABCD的场地,长AB=m米,宽AD=n米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为 .
 17. 已知三条不同的直线a , b , c在同一平面内,下列四个命题:
17. 已知三条不同的直线a , b , c在同一平面内,下列四个命题:①如果a∥b , a⊥c , 那么b⊥c; ②如果b∥a , c∥a , 那么b∥c;
③如果b⊥a , c⊥a , 那么b⊥c; ④如果b⊥a , c⊥a , 那么b∥c .
其中正确的是.(填写序号)
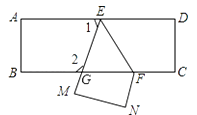
18.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上,若∠EFG=55°,则∠1=°,∠2=°.
 19. 对于有理数x , y定义新运算:x*y=ax+by﹣5,其中a , b为常数已知1*2=﹣9,(﹣3)*3=﹣2,则a﹣b= .20. 我国南宋时期杰出的数学家杨辉是钱塘人,下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了
19. 对于有理数x , y定义新运算:x*y=ax+by﹣5,其中a , b为常数已知1*2=﹣9,(﹣3)*3=﹣2,则a﹣b= .20. 我国南宋时期杰出的数学家杨辉是钱塘人,下面的图表是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了( a + b ) n n 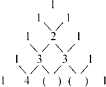
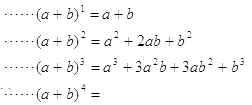 (1)、请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+4ab2+b4
(1)、请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+4ab2+b4
(2)、此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过8 14
三、解答题。
-
21. 计算。(1)、
( − 1 ) 2017 + ( 1 2 ) − 2 + ( 3.14 − π ) 0 (2)、( − 2 x 2 ) 3 + 4 x 3 ⋅ x 3 22. 解方程组。(1)、{ 2 x + 3 y = 7 x = − 2 y + 3 (2)、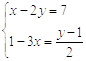 23.
23.如图,已知∠1=∠2,∠B=∠C , 可推得AB∥CD . 理由如下:
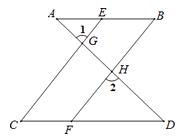
∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已知)
∴(等量代换)
∴AB∥CD()
24.先化简,再求值:
 ,其中
,其中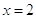 .25. 如图,∠ABD和∠BDC的平分线交于E , BE交CD于点F , ∠1+∠2=90°.
.25. 如图,∠ABD和∠BDC的平分线交于E , BE交CD于点F , ∠1+∠2=90°.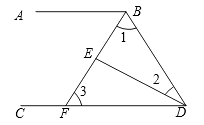 (1)、试说明:AB∥CD;(2)、若∠2=25°,求∠BFC的度数.
(1)、试说明:AB∥CD;(2)、若∠2=25°,求∠BFC的度数.
26. 为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:租金(单位:元/台•时)
挖掘土石方量(单位:m3/台•时)
甲型挖掘机
100
60
乙型挖掘机
120
80
(1)、若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?(2)、如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?