2017年河北省初中毕业生中考数学模拟试卷(3)
试卷更新日期:2017-04-18 类型:中考模拟
一、选择题
-
1. 与﹣3的差为0的数是( )A、3 B、﹣3 C、﹣ D、2. 下列计算正确的是( )A、x2+x3=x5 B、x2•x3=x6 C、(x2)3=x5 D、x5÷x3=x23. 下列图形中,是轴对称图形,但不是中心对称图形的是( )A、
 B、
B、 C、
C、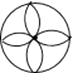 D、
D、 4. 下列等式成立的是( )A、 + = B、 = C、 = D、 =﹣5. 已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )A、k>1,b<0 B、k>1,b>0 C、k>0,b>0 D、k>0,b<06. 设边长为3的正方形的对角线长为a.下列关于a的四种说法:
4. 下列等式成立的是( )A、 + = B、 = C、 = D、 =﹣5. 已知一次函数y=kx+b﹣x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )A、k>1,b<0 B、k>1,b>0 C、k>0,b>0 D、k>0,b<06. 设边长为3的正方形的对角线长为a.下列关于a的四种说法:①a是无理数;
②a可以用数轴上的一个点来表示;
③3<a<4;
④a是18的算术平方根.
其中,所有正确说法的序号是( )
A、①④ B、②③ C、①②④ D、①③④7.有3块积木,每一块的各面都涂上不同的颜色,3块的涂法完全相同,现把它们摆放成不同的位置(如图),请你根据图形判断涂成绿色一面的对面的颜色是( )
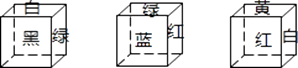 A、白 B、红 C、黄 D、黑8. 绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( )
A、白 B、红 C、黄 D、黑8. 绍兴是著名的桥乡,如图,石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为( ) A、4m B、5m C、6m D、8m9. 用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,作法错误的是( )A、
A、4m B、5m C、6m D、8m9. 用直尺和圆规作Rt△ABC斜边AB上的高线CD,以下四个作图中,作法错误的是( )A、 B、
B、 C、
C、 D、
D、 10. 实数a,b在数轴上的对应点的位置如图所示,把﹣a,﹣b,0按照从小到大的顺序排列,正确的是( )
10. 实数a,b在数轴上的对应点的位置如图所示,把﹣a,﹣b,0按照从小到大的顺序排列,正确的是( )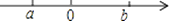 A、﹣a<0<﹣b B、0<﹣a<﹣b C、﹣b<0<﹣a D、0<﹣b<﹣a11. A、B两地相距160千米,甲车和乙车的平均速度之比为4:5,两车同时从A地出发到B地,乙车比甲车早到30分钟,若求甲车的平均速度,设甲车平均速度为4x千米/小时,则所列方程是( )A、 ﹣ =30 B、 ﹣ = C、 ﹣ = D、 + =3012. 在同一平面直角坐标系中,函数y=mx+m与y= (m≠0)的图象可能是( )A、
A、﹣a<0<﹣b B、0<﹣a<﹣b C、﹣b<0<﹣a D、0<﹣b<﹣a11. A、B两地相距160千米,甲车和乙车的平均速度之比为4:5,两车同时从A地出发到B地,乙车比甲车早到30分钟,若求甲车的平均速度,设甲车平均速度为4x千米/小时,则所列方程是( )A、 ﹣ =30 B、 ﹣ = C、 ﹣ = D、 + =3012. 在同一平面直角坐标系中,函数y=mx+m与y= (m≠0)的图象可能是( )A、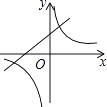 B、
B、 C、
C、 D、
D、 13. 已知命题“关于x的一元二次方程x2+bx+1=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例可以是( )A、b=﹣1 B、b=2 C、b=﹣2 D、b=014. 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
13. 已知命题“关于x的一元二次方程x2+bx+1=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例可以是( )A、b=﹣1 B、b=2 C、b=﹣2 D、b=014. 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( ) A、 B、 C、 D、15. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A、 B、 C、 D、15. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )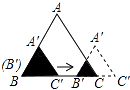 A、
A、 B、
B、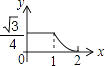 C、
C、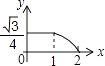 D、
D、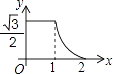
二、填空题
-
16. 计算: ﹣|﹣3|﹣(﹣π)0+2016= .17. 已知a2+3ab+b2=0(a≠0,b≠0),则代数式 + 的值等于 .18. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 , A2n+1的坐标为 .

三、解答题
-
19. 计算下列各题(1)、已知4x=3y,求代数式(x﹣2y)2﹣(x﹣y)(x+y)﹣2y2的值.(2)、计算:π0+2﹣1﹣ ﹣|﹣ |.20. 准备一张矩形纸片,按如图操作:
将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
 (1)、求证:四边形BFDE是平行四边形;(2)、若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.21. △ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
(1)、求证:四边形BFDE是平行四边形;(2)、若四边形BFDE是菱形,AB=2,求菱形BFDE的面积.21. △ABC的顶点坐标为A(﹣2,3)、B(﹣3,1)、C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点. (1)、求过点B′的反比例函数解析式;(2)、求线段CC′的长.22. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)、求过点B′的反比例函数解析式;(2)、求线段CC′的长.22. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: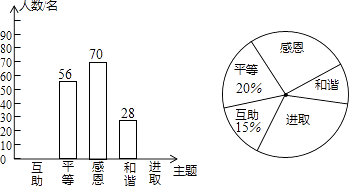 (1)、这次调查的学生共有多少名?(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.(3)、如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).23. 星期天,李玉刚同学随爸爸妈妈回老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km.设爸爸骑行时间为x(h).(1)、请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;(2)、请在同一个平面直角坐标系中画出(1)中两个函数的图象;(3)、请回答谁先到达老家.24. 如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1 , l2重合,AB=4 cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)
(1)、这次调查的学生共有多少名?(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.(3)、如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).23. 星期天,李玉刚同学随爸爸妈妈回老家探望爷爷奶奶,爸爸8:30骑自行车先走,平均每小时骑行20km;李玉刚同学和妈妈9:30乘公交车后行,公交车平均速度是40km/h.爸爸的骑行路线与李玉刚同学和妈妈的乘车路线相同,路程均为40km.设爸爸骑行时间为x(h).(1)、请分别写出爸爸的骑行路程y1(km)、李玉刚同学和妈妈的乘车路程y2(km)与x(h)之间的函数解析式,并注明自变量的取值范围;(2)、请在同一个平面直角坐标系中画出(1)中两个函数的图象;(3)、请回答谁先到达老家.24. 如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm,矩形ABCD的边AD、AB分别与l1 , l2重合,AB=4 cm,AD=4cm,若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s)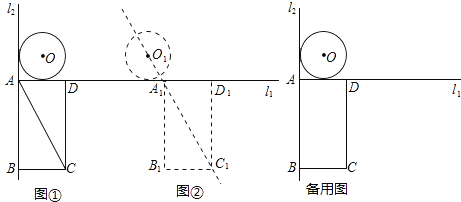 (1)、如图①,连接OA、AC,则∠OAC的度数为°;(2)、如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);(3)、在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).25. 如图①,在平面直角坐标中,点A的坐标为(1,﹣2),点B的坐标为(3,﹣1),二次函数y=﹣x2的图象为l1 .
(1)、如图①,连接OA、AC,则∠OAC的度数为°;(2)、如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,求圆心O移动的距离(即OO1的长);(3)、在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm),当d<2时,求t的取值范围(解答时可以利用备用图画出相关示意图).25. 如图①,在平面直角坐标中,点A的坐标为(1,﹣2),点B的坐标为(3,﹣1),二次函数y=﹣x2的图象为l1 . (1)、平移抛物线l1 , 使平移后的抛物线经过点A,但不过点B.
(1)、平移抛物线l1 , 使平移后的抛物线经过点A,但不过点B.①满足此条件的函数解析式有个.
②写出向下平移且经点A的解析式 .
(2)、平移抛物线l1 , 使平移后的抛物线经过A,B两点,所得的抛物线l2 , 如图②,求抛物线l2的函数解析式及顶点C的坐标,并求△ABC的面积.(3)、在y轴上是否存在点P,使S△ABC=S△ABP?若存在,求出点P的坐标;若不存在,请说明理由.