2017年广西贵港市平南县中考数学一模试卷
试卷更新日期:2017-04-18 类型:中考模拟
一、选择题
-
1. ﹣ 相反数的是( )A、 B、﹣ C、﹣ D、2. 世界上最小的开花结果植物是澳大利亚的出水浮萍,这种植物的果实像一个微笑的无花果,质量只有0.000000076克,将0.000000076克用科学记数法表示为( )A、7.6×10﹣8 B、0.76×10﹣9 C、7.6×108 D、0.76×1093. 下列各式计算正确的是( )A、(a+b)2=a2+b2 B、a•a2=a3 C、a8÷a2=a4 D、a2+a3=a54. 下列命题为真命题的是( )A、有公共顶点的两个角是对顶角 B、多项式x2﹣4x因式分解的结果是x(x2﹣4) C、a+a=a2 D、一元二次方程x2﹣x+2=0无实数根5. 下列各式从左到右的变形中,为因式分解的是( )A、x(a﹣b)=ax﹣bx B、﹣1+=(x﹣1)(x+1)+ C、﹣1=(y+1)(y﹣1) D、ax+by+c=x(a+b)+c6.
如图,观察图形,找出规律,确定第四个图形是( )
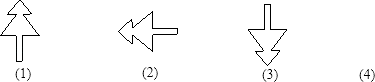 A、
A、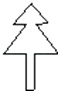 B、
B、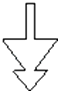 C、
C、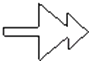 D、
D、 7. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
7. 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )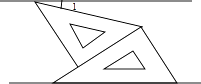 A、30° B、20° C、15° D、14°8. 如图,半圆的圆心为O,直径AB的长为12,C为半圆上一点,∠CAB=30°, 的长是( )
A、30° B、20° C、15° D、14°8. 如图,半圆的圆心为O,直径AB的长为12,C为半圆上一点,∠CAB=30°, 的长是( ) A、12π B、6π C、5π D、4π9. 已知点P(a+1,2a﹣3)关于x轴的对称点在第一象限,则a的取值范围是( )A、a<﹣1 B、﹣1<a< C、﹣ <a<1 D、a>10. 如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A、12π B、6π C、5π D、4π9. 已知点P(a+1,2a﹣3)关于x轴的对称点在第一象限,则a的取值范围是( )A、a<﹣1 B、﹣1<a< C、﹣ <a<1 D、a>10. 如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( ) A、线段DE B、线段PD C、线段PC D、线段PE11. 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( )
A、线段DE B、线段PD C、线段PC D、线段PE11. 如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 函数y= 中,自变量x的取值范围是 .13. 若α、β是方程x2+2x﹣2017=0的两个实数根,则α2+3α+β的值为 .14. 如图,OD是⊙O的半径,弦AB⊥OD于E,若∠O=70°,则∠A+∠C=度.
 15. 如图,P是Rt△ABC的斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有条.
15. 如图,P是Rt△ABC的斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有条. 16. 不论m取任何实数,抛物线y=(x﹣m)2+m﹣1(x为自变量)的顶点都在一条直线上,则这条直线的函数解析式是 .17. 如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= .
16. 不论m取任何实数,抛物线y=(x﹣m)2+m﹣1(x为自变量)的顶点都在一条直线上,则这条直线的函数解析式是 .17. 如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= .
三、解答题
-
18. 计算下面各题(1)、计算:| ﹣2|+20150﹣( )+3tan30°;(2)、解不等式组: ,并将不等式组的解集在所给数轴上表示出来.
 19. 已知BD平分∠ABF,且交AE于点D.(1)、求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);(2)、设AP交BD于点O,交BF于点C,当AC⊥BD时,AD与BC的位置和数量关系是 .
19. 已知BD平分∠ABF,且交AE于点D.(1)、求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);(2)、设AP交BD于点O,交BF于点C,当AC⊥BD时,AD与BC的位置和数量关系是 . 20. 已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P( ,n),Q(4,m)两点,且tan∠BOP= :
20. 已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P( ,n),Q(4,m)两点,且tan∠BOP= : (1)、求反比例函数和直线的函数表达式;(2)、求△OPQ的面积.21. 某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
(1)、求反比例函数和直线的函数表达式;(2)、求△OPQ的面积.21. 某中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:跳绳数/个
81
85
90
93
95
98
100
人 数
1
2
8
11
5
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
 (1)、将表中空缺的数据填写完整,并补全频数分布直方图;(2)、这个班同学这次跳绳成绩的众数是个,中位数是个;(3)、若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.
(1)、将表中空缺的数据填写完整,并补全频数分布直方图;(2)、这个班同学这次跳绳成绩的众数是个,中位数是个;(3)、若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.
22. 某工厂对零件进行检测,引进了检测机器.已知一台检测机的工作效率相当于一名检测员的20倍.若用这台检测机检测900个零件要比15名检测员检测这些零件少3小时.(1)、求一台零件检测机每小时检测零件多少个?(2)、现有一项零件检测任务,要求不超过7小时检测完成3450个零件.该厂调配了2台检测机和30名检测员,工作3小时后又调配了一些检测机进行支援,则该厂至少再调配几台检测机才能完成任务?23. 如图,△ABC中,E是AC上一点,且AE=AB,∠EBC= ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F. (1)、求证:BC与⊙O相切;(2)、若AB=8,sin∠EBC= ,求AC的长.24. 如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点.
(1)、求证:BC与⊙O相切;(2)、若AB=8,sin∠EBC= ,求AC的长.24. 如图,在矩形ABCD中,AO=10,AB=8,分别以OC、OA所在的直线为x轴,y轴建立平面直角坐标系,点D(3,10)、E(0,6),抛物线y=ax2+bx+c经过O,D,C三点. (1)、求抛物线的解析式;(2)、一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)、点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使四边形MENC是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.25. 在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(1)、求抛物线的解析式;(2)、一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动.设运动时间为t秒,当t为何值时,以P、Q、C为顶点的三角形与△ADE相似?(3)、点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使四边形MENC是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.25. 在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′. (2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
