2017年广东省深圳市南山区十校联考中考数学一模试卷

试卷更新日期：2017-04-18 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个数中，无理数是（）

A、﹣ $\frac{2}{3}$ B、﹣ $\sqrt{3}$ C、0 D、|﹣2|

查看试题解析
2. 下列全国各地地铁标志图中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 过度包装既浪费资源又污染环境，据测算，如果全国每年减少十分之一的包装纸用量，那么能减少3120000吨二氧化碳的排放量，把数据3120000用科学记数法表示为（）

A、312×10⁴ B、0.312×10⁷ C、3.12×10⁶ D、3.12×10⁷

查看试题解析
4. 下列运算结果为a⁶的是（）

A、a²+a³ B、a²•a³ C、（﹣a²）³ D、a⁸÷a²

查看试题解析
5. 如图，AD是∠EAC的平分线，AD∥BC，∠B=30°，则∠C的度数为（）

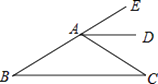A、50° B、40° C、30° D、20°

查看试题解析
6. 请仔细观察用直尺和圆规作一个角∠A′O′B′等于已知角∠AOB的示意图，要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是（）

A、边边边 B、边角边 C、角边角 D、角角边

查看试题解析
7. 对于双曲线y= $\frac{1 - m}{x}$ ，当x＞0时，y随x的增大而减小，则m的取值范围为（）

A、m＞0 B、m＞1 C、m＜0 D、m＜1

查看试题解析
8. 某单位组织34人分别到井冈山和瑞金进行革命传统教育，到井冈山的人数是到瑞金的人数的2倍多1人，求到两地的人数各是多少？设到井冈山的人数为x人，到瑞金的人数为y人．下面所列的方程组正确的是（）

A、 ${\begin{matrix} x + y = 34 \\ x + 1 = 2 y \end{matrix}$ B、 ${\begin{matrix} x + y = 34 \\ x = 2 y + 1 \end{matrix}$ C、 ${\begin{matrix} x + y = 34 \\ 2 x = y + 1 \end{matrix}$ D、 ${\begin{matrix} x + 2 y = 34 \\ x = 2 y + 1 \end{matrix}$

查看试题解析
9. 如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则 $\overset{⌢}{B C}$ 的长为（）

A、 $\frac{10}{3}$ π B、 $\frac{10}{9}$ π C、 $\frac{5}{9}$ π D、 $\frac{5}{18}$ π

查看试题解析
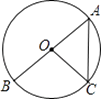10. 下列命题正确是（）

A、点（1，3）关于x轴的对称点是（﹣1，3） B、函数 y=﹣2x+3中，y随x的增大而增大 C、若一组数据3，x，4，5，6的众数是3，则中位数是3 D、同圆中的两条平行弦所夹的弧相等

查看试题解析
11. 下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（）

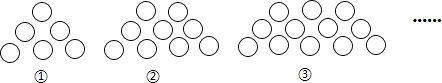A、21 B、24 C、27 D、30

查看试题解析
12. 如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交AF于点G，连接DG．给出以下结论：①DG=DF；②四边形EFDG是菱形；③EG²= $\frac{1}{2}$ GF×AF；④当AG=6，EG=2 $\sqrt{5}$ 时，BE的长为 $\frac{12}{5}$ $\sqrt{5}$ ，其中正确的结论个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

13. 分解因式：2x²﹣8= ．

查看试题解析
14. 小明用S²= $\frac{1}{10}$ [（x₁﹣3）²+（x₂﹣3）²+…+（x₁₀﹣3）³]计算一组数据的方差，那么x₁+x₂+x₃+…+x₁₀= ．

查看试题解析
15. 如图，测量河宽AB（假设河的两岸平行），在C点测得∠ACB=30°，D点测得∠ADB=60°，又CD=60m，则河宽AB为m（结果保留根号）．

查看试题解析
16. 如图，10个边长为1的正方形如图摆放在平面直角坐标系中，经过原点的一条直线l将这10个正方形分成面积相等的两部分，则该直线l的解析式为．

查看试题解析

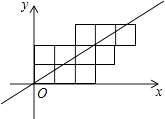
三、解答题

17. 计算：2cos60°﹣（﹣3）^﹣³+（π﹣ $\sqrt{3}$ ）⁰﹣|﹣2|．

查看试题解析
18. 先化简，再求值：（1﹣ $\frac{1}{a + 1}$ ）÷ $\frac{a}{a^{2} + 2 a + 1}$ ，其中a= $\sqrt{3}$ ﹣1．

查看试题解析
19. “赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别
成绩x分
频数（人数）
第1组
50≤x＜60
6
第2组
60≤x＜70
8
第3组
70≤x＜80
14
第4组
80≤x＜90
a
第5组
90≤x＜100
10
请结合图表完成下列各题：

(1)、①求表中a的值；②频数分布直方图补充完整；

(2)、若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？

(3)、第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率．

查看试题解析
20.
如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y= $\frac{k}{x}$ （k＞0）的图象与BC边交于点E．

(1)、当F为AB的中点时，求该函数的解析式；

(2)、当k为何值时，△EFA的面积最大，最大面积是多少？

查看试题解析
21. 某家电销售商城电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等．

(1)、求每台电冰箱与空调的进价分别是多少？

(2)、现在商城准备一次购进这两种家电共100台，设购进电冰箱x台，这100台家电的销售总利润为y元，要求购进空调数量不超过电冰箱数量的2倍，总利润不低于13000元，请分析合理的方案共有多少种？并确定获利最大的方案以及最大利润．

查看试题解析
22.
已知，如图（1），PAB为⊙O的割线，直线PC与⊙O有公共点C，且PC²=PA×PB，

(1)、求证：∠PCA=∠PBC；直线PC是⊙O的切线；

(2)、
如图（2），作弦CD，使CD⊥AB，连接AD、BC，若AD=2，BC=6，求⊙O的半径；

(3)、
如图（3），若⊙O的半径为 $\sqrt{2}$ ，PO= $\sqrt{10}$ ，MO=2，∠POM=90°，⊙O上是否存在一点Q，使得PQ+ $\frac{\sqrt{2}}{2}$ QM有最小值？若存在，请求出这个最小值；若不存在，说明理由．

查看试题解析
23.
在平面直角坐标系中，抛物线y=ax²﹣5ax+4a与x轴交于A、B（A点在B点的左侧）与y轴交于点C．

(1)、如图1，连接AC、BC，若△ABC的面积为3时，求抛物线的解析式；

(2)、如图2，点P为第四象限抛物线上一点，连接PC，若∠BCP=2∠ABC时，求点P的横坐标；

(3)、如图3，在（2）的条件下，点F在AP上，过点P作PH⊥x轴于H点，点K在PH的延长线上，AK=KF，∠KAH=∠FKH，PF=﹣4 $\sqrt{2}$ a，连接KB并延长交抛物线于点Q，求PQ的长．

查看试题解析

组别	成绩x分	频数（人数）
第1组	50≤x＜60	6
第2组	60≤x＜70	8
第3组	70≤x＜80	14
第4组	80≤x＜90	a
第5组	90≤x＜100	10