2017年广东省佛山市顺德区中考数学一模试卷
试卷更新日期:2017-04-18 类型:中考模拟
一、选择题
-
1. y=x2+2的对称轴是直线( )A、x=2 B、x=0 C、y=0 D、y=22. 抛物线y=2(x﹣3)2+1的顶点坐标是( )A、(3,1) B、(3,﹣1) C、(﹣3,1) D、(﹣3,﹣1)3. 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
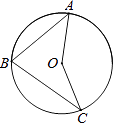 A、120° B、130° C、140° D、150°4. 在Rt△ABC中,∠C=90°,a=1,b= ,则∠A=( )A、30° B、45° C、60° D、90°5. 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
A、120° B、130° C、140° D、150°4. 在Rt△ABC中,∠C=90°,a=1,b= ,则∠A=( )A、30° B、45° C、60° D、90°5. 如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )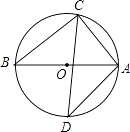 A、20° B、40° C、50° D、70°6. 如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )
A、20° B、40° C、50° D、70°6. 如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是( )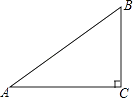 A、msin35° B、mcos35° C、 D、7. 已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )A、k<4 B、k≤4 C、k<4且k≠3 D、k≤4且k≠38. 如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )
A、msin35° B、mcos35° C、 D、7. 已知函数y=(k﹣3)x2+2x+1的图象与x轴有交点,则k的取值范围是( )A、k<4 B、k≤4 C、k<4且k≠3 D、k≤4且k≠38. 如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( )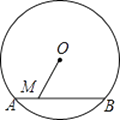 A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<59. 在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )A、
A、3≤OM≤5 B、4≤OM≤5 C、3<OM<5 D、4<OM<59. 在同一坐标系中一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )A、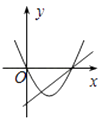 B、
B、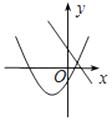 C、
C、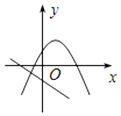 D、
D、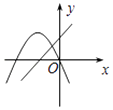
二、填空题
-
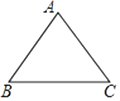
10. 已知⊙O的半径为3cm,圆心O到直线l的距离是2m,则直线l与⊙O的位置关系是 .11. 把抛物线y=﹣x2向左平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为 .12. 如图,等腰△ABC的周长是36cm,底边为10cm,则底角的正切值是 .
 13. 如图,扇形OAB的圆心角为120°,半径为3cm,则该扇形的弧长为 cm,面积为 cm2 . (结果保留π)
13. 如图,扇形OAB的圆心角为120°,半径为3cm,则该扇形的弧长为 cm,面积为 cm2 . (结果保留π) 14. 如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,若其与x轴一交点为A(3,0),则由图象可知,不等式ax2+bx+c<0的解集是 .
14. 如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,若其与x轴一交点为A(3,0),则由图象可知,不等式ax2+bx+c<0的解集是 . 15. 抛物线的顶点在(1,﹣2),且过点(2,3),则函数的关系式:
15. 抛物线的顶点在(1,﹣2),且过点(2,3),则函数的关系式:三、解答题
-
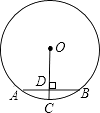
16. 计算:2﹣1+ cos30°+|﹣5|﹣(π﹣2017)0 .17. 如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=l,求⊙O的半径.
 18. 某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?
18. 某商店购买一批单价为20元的日用品,如果以单价30元销售,那么半月内可以售出400件.据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高一元,销售量相应减少20件.如何提高销售价,才能在半月内获得最大利润?四、解答题
-
19. 校运会上,小明参加铅球比赛,若某次试掷,铅球飞行的高度y(m)与水平距离x(m)之间的函数关系式为y=﹣ x2+ x+ ,求:
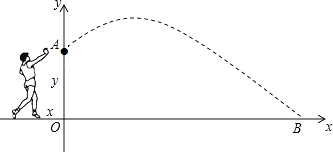 (1)、铅球的出手时的高度;(2)、小明这次试掷的成绩.20.
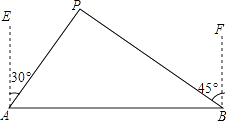
(1)、铅球的出手时的高度;(2)、小明这次试掷的成绩.20.如图所示,A、B两城市相距100km,现计划在这两座城市间修建一条高速公路(即线段AB),经测量,森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上,已知森林保护区的范围在以P点为圆心,50km为半径的圆形区域内,请问计划修建的这条高速公路会不会穿越保护区,为什么?(参考数据: ≈1.732, ≈1.414)
 21. 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD. 与 的大小有什么关系?为什么?
21. 如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD. 与 的大小有什么关系?为什么?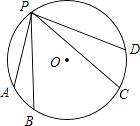
五、解答题
-
22. 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,S四边形DEFG=y.
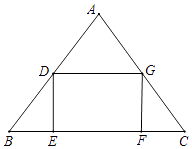 (1)、填空:自变量x的取值范围是;(2)、求出y与x的函数表达式;(3)、请描述y随x的变化而变化的情况.23. 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.
(1)、填空:自变量x的取值范围是;(2)、求出y与x的函数表达式;(3)、请描述y随x的变化而变化的情况.23. 如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE.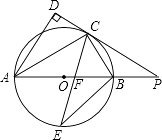 (1)、求证:AC平分∠DAB;(2)、探究线段PC,PF之间的大小关系,并加以证明;(3)、若tan∠PCB= ,BE= ,求PF的长.24.
(1)、求证:AC平分∠DAB;(2)、探究线段PC,PF之间的大小关系,并加以证明;(3)、若tan∠PCB= ,BE= ,求PF的长.24.如图,抛物线经过A(﹣1,0),B(5,0),C(0, )三点.
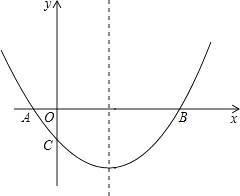 (1)、求抛物线的解析式;(2)、在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)、点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)、点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.