2017年安徽省淮北市濉溪县中考数学一模试卷
试卷更新日期:2017-04-18 类型:中考模拟
一、选择题
-
1. 已知5x=6y(y≠0),那么下列比例式中正确的是( )A、 B、 C、 D、2. 在下面的四个几何体中,它们各自的主视图与左视图可能不相同的是( )A、
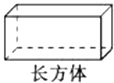 B、
B、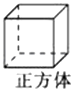 C、
C、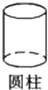 D、
D、 3. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=34. 若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式是( )A、y=(x﹣2)2﹣3 B、y=(x﹣2)2+3 C、y=(x+2)2﹣3 D、y=(x+2)2+35. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( )
3. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=34. 若将抛物线y=x2向右平移2个单位,再向上平移3个单位,则得到的抛物线解析式是( )A、y=(x﹣2)2﹣3 B、y=(x﹣2)2+3 C、y=(x+2)2﹣3 D、y=(x+2)2+35. 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是( ) A、 B、 C、 D、6. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )
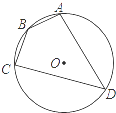
A、 B、 C、 D、6. 如图,A、D是⊙O上的两个点,BC是直径,若∠D=32°,则∠OAC等于( )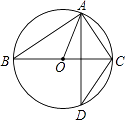 A、64° B、58° C、68° D、55°7. 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA , 则△ABC与△DEF的面积之比为( )
A、64° B、58° C、68° D、55°7. 如图,以点O为位似中心,将△ABC放大得到△DEF.若AD=OA , 则△ABC与△DEF的面积之比为( )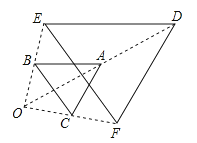 A、1:2 B、1:4 C、1:5 D、1:68. 如图,已知反比例函数y= (x>0),则k的取值范围是( )
A、1:2 B、1:4 C、1:5 D、1:68. 如图,已知反比例函数y= (x>0),则k的取值范围是( )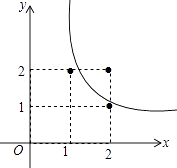 A、1<k<2 B、2<k<3 C、2<k<4 D、2≤k≤49. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A、1<k<2 B、2<k<3 C、2<k<4 D、2≤k≤49. 如图,⊙O的半径为2,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )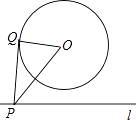 A、 B、 C、3 D、210.
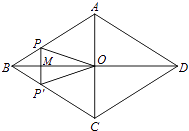
A、 B、 C、3 D、210.如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
 A、
A、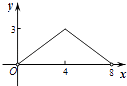 B、
B、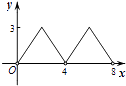 C、
C、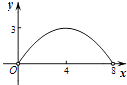 D、
D、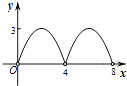
二、填空题
-
11. 计算:tan45°﹣2cos60°= .12. 如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则 的长 .
 13. 在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2 ,AB=3,则AD= .
13. 在△ABC中,D为AB边上一点,且∠BCD=∠A,已知BC=2 ,AB=3,则AD= .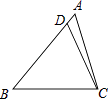 14. 二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
14. 二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表x
﹣1
0
1
3
y
﹣1
3
5
3
下列结论:①ac<0;②当x>1时,y的值随x值的增大而减小.
③当x=2时,y=5;④3是方程ax2+(b﹣1)x+c=0的一个根;
其中正确的有 . (填正确结论的序号)
三、解答题
-
15. 解方程:x(x﹣4)=1.16.
如图,在小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,根据图形解答下列问题:
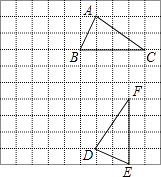 (1)、将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△A1B1C1;(2)、将△DEF绕D点逆时针旋转90°,画出旋转后的△DE1F1 .17. 某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据: ≈1.41, ≈1.73,60千米/时= 米/秒)
(1)、将△ABC向左平移4个单位长度,再向下平移2个单位长度,画出平移后的△A1B1C1;(2)、将△DEF绕D点逆时针旋转90°,画出旋转后的△DE1F1 .17. 某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据: ≈1.41, ≈1.73,60千米/时= 米/秒)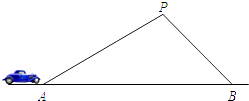 18.
18.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”,已知点A、B、C、D分别是“果圆”与坐标轴的交点,AB为半圆的直径,抛物线的解析式为y=x2﹣2x﹣3,求这个“果圆”被y轴截得线段CD的长
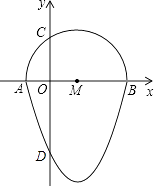 19. 某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
19. 某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.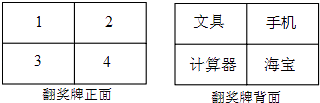 (1)、如果甲先抽奖,那么甲获得“手机”的概率是多少?(2)、小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.20. 某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.(1)、用含x的代数式表示第3年的可变成本为万元;(2)、如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.21. 如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.
(1)、如果甲先抽奖,那么甲获得“手机”的概率是多少?(2)、小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.20. 某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均每年增长的百分率为x.(1)、用含x的代数式表示第3年的可变成本为万元;(2)、如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.21. 如图,在等腰直角△ABC中,∠ACB=90°,点D为三角形内一点,且∠ACD=∠DAB=∠DBC.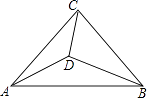 (1)、求∠CDB的度数;(2)、求证:△DCA∽△DAB;(3)、若CD的长为1,求AB的长.22. 2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.
(1)、求∠CDB的度数;(2)、求证:△DCA∽△DAB;(3)、若CD的长为1,求AB的长.22. 2016年里约奥运会,中国跳水队赢得8个项目中的7块金牌,优秀成绩的取得离不开艰辛的训练.某跳水运动员在进行跳水训练时,身体(看成一点)在空中的运动路线是如图所示的一条抛物线,已知跳板AB长为2米,跳板距水面CD的高BC为3米,训练时跳水曲线在离起跳点水平距离1米时达到距水面最大高度k米,现以CD为横轴,CB为纵轴建立直角坐标系.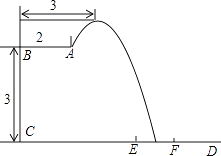 (1)、当k=4时,求这条抛物线的解析式;(2)、当k=4时,求运动员落水点与点C的距离;(3)、图中CE= 米,CF= 米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.23. [发现]如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
(1)、当k=4时,求这条抛物线的解析式;(2)、当k=4时,求运动员落水点与点C的距离;(3)、图中CE= 米,CF= 米,若跳水运动员在区域EF内(含点E,F)入水时才能达到训练要求,求k的取值范围.23. [发现]如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
[思考]如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的⊙O上吗?
我们知道,如果点D不在经过A,B,C三点的圆上,那么点D要么在⊙O外,要么在⊙O内,以下该同学的想法说明了点D不在⊙O外.请结合图④证明点D也不在⊙O内.
【证】
[结论]综上可得结论,如果∠ACB=∠ADB=α(点C,D在AB的同侧),那么点D在经过A,B,C三点的圆上,即:A、B、C、D四点共圆.
[应用]利用上述结论解决问题:
如图⑤,已知△ABC中,∠C=90°,将△ACB绕点A顺时针旋转α度(α为锐角)得△ADE,连接BE、CD,延长CD交BE于点F;
(1)、用含α的代数式表示∠ACD的度数;(2)、求证:点B、C、A、F四点共圆;(3)、求证:点F为BE的中点.