广东省深圳市宝安、罗湖、福田、龙华四区2018-2019学年七年级上学期数学期中考试试卷
试卷更新日期:2019-02-18 类型:期中考试
一、选择题
-
1. 6的绝对值是( )A、
 B、
B、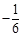 C、
C、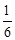 D、6
2. 共享单车为市民短距离出行带来了极大便利.据2018年“深圳互联网自行车发展评估报告”披露,深圳市日均使用共享单车2590000人次,其中2590000用科学记数法表示为( )A、259×104 B、25.9×105 C、2.59×106 D、0.259×1073. 下列各式符合代数式书写规范的是( )A、
D、6
2. 共享单车为市民短距离出行带来了极大便利.据2018年“深圳互联网自行车发展评估报告”披露,深圳市日均使用共享单车2590000人次,其中2590000用科学记数法表示为( )A、259×104 B、25.9×105 C、2.59×106 D、0.259×1073. 下列各式符合代数式书写规范的是( )A、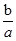 B、a×7
C、2m﹣1元
D、3
B、a×7
C、2m﹣1元
D、3 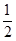 x
4. 在式子a2+2, ,ab2 , ,﹣8x,0中,整式有( )A、3个 B、4个 C、5个 D、6个5. 如图所示,用一个平面分别去截下列水平放置的几何体,所截得的截面不可能是三角形的是( )A、
x
4. 在式子a2+2, ,ab2 , ,﹣8x,0中,整式有( )A、3个 B、4个 C、5个 D、6个5. 如图所示,用一个平面分别去截下列水平放置的几何体,所截得的截面不可能是三角形的是( )A、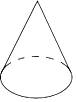 B、
B、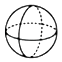 C、
C、 D、
D、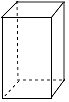 6. 下列计算正确的是( )A、3x2y﹣2x2y=x2y B、5y﹣3y=2 C、3a+2b=5ab D、7a+a=7a27. 下列各组数中,不是互为相反数的是( )A、
6. 下列计算正确的是( )A、3x2y﹣2x2y=x2y B、5y﹣3y=2 C、3a+2b=5ab D、7a+a=7a27. 下列各组数中,不是互为相反数的是( )A、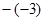 与
与 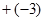 B、
B、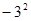 与
与  C、
C、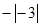 与
与 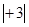 D、
D、 与
与 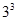 8. 下列结论中,正确的是( )A、单项式
8. 下列结论中,正确的是( )A、单项式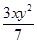 的系数是3,次数是2.
B、单项式m的次数是1,没有系数.
C、单项式﹣xy2z的系数是﹣1,次数是4.
D、多项式5x2-xy+3是三次三项式.
9. 若x2+3x﹣5的值为7,则3x2+9x﹣2的值为( )A、44 B、34 C、24 D、1410. 若 | | =- ,则 一定是( )A、非正数 B、正数 C、非负数 D、负数11. 随着计算机技术的迅猛发展,电脑价格不断降低,某品牌的电脑按原价降低 元后又降 ,现售价为 元,那么该电脑的原售价为( )A、
的系数是3,次数是2.
B、单项式m的次数是1,没有系数.
C、单项式﹣xy2z的系数是﹣1,次数是4.
D、多项式5x2-xy+3是三次三项式.
9. 若x2+3x﹣5的值为7,则3x2+9x﹣2的值为( )A、44 B、34 C、24 D、1410. 若 | | =- ,则 一定是( )A、非正数 B、正数 C、非负数 D、负数11. 随着计算机技术的迅猛发展,电脑价格不断降低,某品牌的电脑按原价降低 元后又降 ,现售价为 元,那么该电脑的原售价为( )A、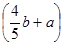 元
B、
元
B、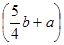 元
C、
元
C、 元
D、
元
D、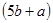 元
12. 用同样大小的围棋子按如图所示的方式摆图案,按照这样的规律摆下去,第12个图案的围棋子个数是( )
元
12. 用同样大小的围棋子按如图所示的方式摆图案,按照这样的规律摆下去,第12个图案的围棋子个数是( ) A、16 B、28 C、29 D、38
A、16 B、28 C、29 D、38二、填空题
-
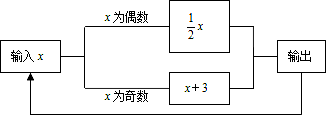
13. 的倒数是;14. 如图所示的运算程序中,若开始输入的x值为16,我们发现第一次输出的结果为8,第二次输出的结果为4,…,则第2017输出的结果为;
 15. p在数轴上的位置如图所示, 化简: =;
15. p在数轴上的位置如图所示, 化简: =;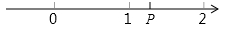 16. x,y表示两个数,规定新运算“※”及“△”如下:x※y=6x+5y,x△y=3xy,则(﹣2※3)△(﹣4)= .
16. x,y表示两个数,规定新运算“※”及“△”如下:x※y=6x+5y,x△y=3xy,则(﹣2※3)△(﹣4)= .三、解答题
-
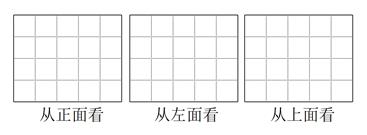
17. 计算:(1)、(2)、18. 先化简,再求值:x2﹣(5x2﹣4y)+3(x2﹣y),其中x=﹣1,y=2.19. 如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图.
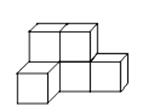 20. 检修队乘汽车沿着东西走向的公路往返行驶检修线路.某天早上从A地出发到收工时所走的路线为(若约定向东为正方向),当天行驶的记录如下:(单位:km)
20. 检修队乘汽车沿着东西走向的公路往返行驶检修线路.某天早上从A地出发到收工时所走的路线为(若约定向东为正方向),当天行驶的记录如下:(单位:km)+18,﹣9.5,+7,﹣14,﹣6.2,+13,﹣6.8,+10.5.
(1)、收工时距A地多远?(2)、若汽车行驶每千米耗油0.3升,那么这一天共耗油多少升?21. 某移动通讯公司开设了两种通讯业务,“全球通”:使用时首先缴 元月租费,然后每通话 分钟,自付话费 元;“动感地带”:不缴月租费,每通话 分钟,付话费 元(本题的通话费均指市内话费),若一个月通话 分钟,两种方式的费用分别表示M元和N元.(1)、用含x的代数式分别表示M和N,则M= , N= .(2)、某人估计一个月内通话 分钟,应选择哪种移动通讯合算些?22. 小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题: (1)、用含x、y的代数式表示地面总面积;(2)、若x=5,y= ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?23.(1)、①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是;根据此规律,如果 ( 为正整数)表示这个数列的第 项,那么 , ;
(1)、用含x、y的代数式表示地面总面积;(2)、若x=5,y= ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?23.(1)、①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是;根据此规律,如果 ( 为正整数)表示这个数列的第 项,那么 , ;②如果欲求 的值,可令
……………①
将①式右边顺序倒置,得 ……………②
由②加上①式,得2 ;
∴ S=;
由结论求 =;
(2)、①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ▲ ;根据此规律,如果 ( 为正整数)表示这个数列的第 项,那么 ▲ , ▲ ;②为了求 的值,可令 ,则 ,因此 ,所以 ,
即 .
仿照以上推理,计算