2017年安徽省滁州市全椒县中考数学一模试卷

试卷更新日期：2017-04-18 类型：中考模拟

进入出卷网下载

一、选择题

1. 若反比例函数y= $\frac{k}{x}$ 的图象经过点（2，﹣1），则k的值为（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 二次函数y=x²﹣2x的顶点为（）

A、（1，1） B、（2，﹣4） C、（﹣1，1） D、（1，﹣1）

查看试题解析
3. 如图，在Rt△ABC中，∠C=90°，AB=2BC，则sinB的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
4. 如图，将一个小球摆放在圆柱上底面的正中间，则该几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
5. 从分别标有数﹣3，﹣2，﹣1，1，2，3的六张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数的绝大于﹣2的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 某人沿斜坡坡度i=1：2的斜坡向上前进了6米，则他上升的高度为（）

A、3米 B、 $\frac{6 \sqrt{5}}{5}$ 米 C、2 $\sqrt{3}$ 米 D、 $\frac{12 \sqrt{5}}{5}$ 米

查看试题解析
7. 已知二次函数y=（k﹣2）x²+2x+1的图象与x轴有交点，则k的取值范围是（）

A、k≥3 B、k＜3 C、k≤3且k≠2 D、k＜2

查看试题解析
8. 如图，在矩形ABCD中，AB=6，BC=8，点E在对角线BD上，且BE=6，连接AE并延长交DC于点F，则CF等于（）

A、2 B、3 C、4 D、5

查看试题解析
9.
如图，在扇形AOB中，∠AOB=90°， $\overset{⌢}{A C}$ = $\overset{⌢}{B C}$ ，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2 $\sqrt{2}$ 时，则阴影部分的面积为（）

A、2π﹣4 B、4π﹣8 C、2π﹣8 D、4π﹣4

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，其对称轴为x=1，则下列结论中错误的是（）

A、abc＜0 B、a﹣b+c＜0 C、b²﹣4ac＞0 D、3a+c＞0

查看试题解析

二、填空题

11. 二次函数y=x²+1的最小值是．

查看试题解析
12. 如图，点A、B、C在⊙O上，∠A=36°，则∠O= ．

查看试题解析
13. 如图，△ABC与△A′B′C′都是等腰三角形，且AB=AC=5，A′B′=A′C′=3，若∠B+∠B′=90°，则△ABC与△A′B′C′的面积比为．

查看试题解析
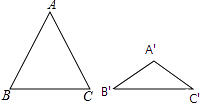14. 如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后，折痕DE分别交AB，AC于点E、G，连接GF，有下列结论：
①∠AGD=112.5°；②tan∠AED= $\sqrt{2}$ +1；③四边形AEFG是菱形；④S_△_ACD= $\sqrt{3}$ S_△_OCD ．
其中正确结论的序号是．（把所有正确结论的序号都填在横线上）

查看试题解析

三、解答题

15. 计算：2cos60°﹣| $\sqrt{2}$ ﹣4sin45°|

查看试题解析
16. 如图，在△ABC中，∠BAC=45°，AB=AC，D为△ABC内一点，AD=4，如果把△ABD绕点A按逆时针方向旋转，使AB与AC重合，求点D运动的路径长．

查看试题解析

四、解答题

17. 如图，⊙O的半径为2，弦AB=2 $\sqrt{3}$ ，点C在弦AB上，AC= $\frac{1}{4}$ AB，求OC的长．

查看试题解析
18. 某校举办校级篮球赛，进入决赛的队伍有A、B、C、D，要从中选出两队打一场比赛．

(1)、若已确定A打第一场，再从其余三队中随机选取一队，求恰好选中D队的概率．

(2)、请用画树状图或列表法，求恰好选中B、C两队进行比赛的概率．

查看试题解析

五、解答题

19. 要在宽为36m的公路的绿化带MN（宽为4m）的中央安装路灯，路灯的灯臂AD的长为3m，且与灯柱CD成120°（如图所示），路灯采用圆锥形灯罩，灯罩的轴线AB与灯臂垂直．当灯罩的轴线通过公路路面一侧的中间时（除去绿化带的路面部分），照明效果最理想，问：应设计多高的灯柱，才能取得最理想的照明效果？（精确到0.01m，参考数据 $\sqrt{3}$ ≈1.732）

查看试题解析
20. 如图，在平面直角坐标系中，已知反比例函数y= $\frac{k}{x}$ （x＞0）的图象和菱形OABC，且OB=4，tan∠BOC= $\frac{1}{2}$ ．

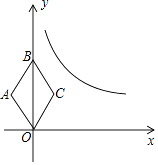(1)、求A、B、C三点的坐标；

(2)、若将菱形向右平移，菱形的两个顶点恰好同时落在反比例函数的图象上，猜想这是哪两个点，并求菱形的平移距离和反比例函数的解析式．

查看试题解析

六、解答题

21. 如图，OA是⊙M的直径，点B在x轴上，连接AB交⊙M于点C．

(1)、若点A的坐标为（0，2），∠ABO=30°，求点B的坐标．

(2)、若D为OB的中点，求证：直线CD是⊙O的切线．

查看试题解析

七、解答题

22.
如图，抛物线的顶点为C（1，﹣2），直线y=kx+m与抛物线交于A、B来两点，其中A点在x轴的正半轴上，且OA=3，B点在y轴上，点P为线段AB上的一个动点（点P与点A、B不重合），过点P且垂直于x轴的直线与这条抛物线交于点E．

(1)、求直线AB的解析式．

(2)、设点P的横坐标为x，求点E的坐标（用含x的代数式表示）．

(3)、求△ABE面积的最大值．

查看试题解析

八、解答题

23.
如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为（﹣8，0），点B的坐标为（﹣8，6），直线BC∥x轴，交y轴于点C，将四边形OABC绕点O按顺时针方向旋转α度得到四边形OA′B′C′，此时直线OA′、直线B′C′分别与直线BC相交于点P、Q．

(1)、四边形OABC的形状是，当α=90°时， $\frac{B P}{B Q}$ 的值是．

(2)、
①如图2，当四边形OA′B′C′的顶点B′落在y轴正半轴上时，求 $\frac{B P}{B Q}$ 的值；
②如图3，当四边形OA′B′C′的顶点B′落在BC的延长线上时，求△OPB′的面积．

(3)、在四边形OABC旋转过程中，当0°＜α≤180°时，是否存在这样的点P和点Q，使BP= $\frac{1}{2}$ BQ？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析