天津市蓟州等部分区2018-2019学年高三上学期文数期末联考试卷
试卷更新日期:2019-02-18 类型:期末考试
一、单选题
-
1. 设全集 , , ,则 ( )A、
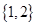 B、
B、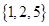 C、
C、 D、
D、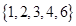 2. 设变量 满足约束条件 则目标函数 的最小值为( )A、1 B、2 C、7 D、83. 阅读如图的程序框图,运行相应的程序,则输出 的值为( )
2. 设变量 满足约束条件 则目标函数 的最小值为( )A、1 B、2 C、7 D、83. 阅读如图的程序框图,运行相应的程序,则输出 的值为( ) A、8 B、4 C、
A、8 B、4 C、 D、
D、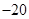 4. 已知 ,则 的大小关系为( )A、
4. 已知 ,则 的大小关系为( )A、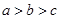 B、
B、 C、
C、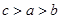 D、
D、 5. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件6. 在 中, 为 的中点, ,则 ( )A、 B、
5. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件6. 在 中, 为 的中点, ,则 ( )A、 B、 C、3
D、
C、3
D、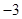 7. 函数 (其中 )的图象如图所示,为了得到函数 的图象,只需将 的图象上所有点( )
7. 函数 (其中 )的图象如图所示,为了得到函数 的图象,只需将 的图象上所有点( ) A、向右平移
A、向右平移 个单位长度
B、向左平移
个单位长度
B、向左平移  个单位长度
C、向右平移 个单位长度
D、向左平移 个单位长度
8. 已知双曲线 的左、右焦点分别为 ,过点 且垂直于 轴的直线与该双曲线的左支交于 两点, 分别交 轴于 两点,若 的周长为12,则当 取得最大值时,该双曲线的渐近线方程为( )A、
个单位长度
C、向右平移 个单位长度
D、向左平移 个单位长度
8. 已知双曲线 的左、右焦点分别为 ,过点 且垂直于 轴的直线与该双曲线的左支交于 两点, 分别交 轴于 两点,若 的周长为12,则当 取得最大值时,该双曲线的渐近线方程为( )A、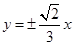 B、
B、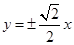 C、
C、 D、
D、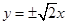
二、填空题
-
9. 是虚数单位,复数 .10. 已知函数 , 是 的导函数,则 .11. 已知长方体的长、宽、高分别为2,1,2,则该长方体外接球的表面积为 .12. 已知直线 与圆 相交于 两点,且线段 的中点P坐标为 ,则直线 的方程为 .13. 已知 ,且 ,若 恒成立,则实数 的取值范围是 .14. 已知函数 若关于 的方程 恰有两个互异的实数解,则实数 的取值范围是 .
三、解答题
-
15. 为维护交通秩序,防范电动自行车被盗,天津市公安局决定,开展二轮电动自行车免费登记、上牌照工作.电动自行车牌照分免费和收费(安装防盗装置)两大类,群众可以 自愿选择安装.已知甲、乙、丙三个不同类型小区的人数分别为15000,15000,20000.交管部门为了解社区居民意愿,现采用分层抽样的方法从中抽取10人进行电话访谈.
(Ⅰ)应从甲小区和丙小区的居民中分别抽取多少人?
(Ⅱ)设从甲小区抽取的居民为 ,丙小区抽取的居民为 .现从甲小区和丙小区已抽取的居民中随机抽取2人接受问卷调查.
(ⅰ)试用所给字母列举出所有可能的抽取结果;
(ⅱ)设 为事件“抽取的2人来自不同的小区”,求事件 发生的概率.
16. 在 中,内角A,B,C所对的边分别为a,b,c已知 .1 求角C的大小
17. 如图,四棱锥 中,底面四边形 为菱形, , 为等边三角形.
(Ⅰ)求证: ;
(Ⅱ)若 ,求直线 与平面 所成的角.