广东省揭阳市揭西县2018-2019学年九年级上学期数学期末考试试卷

试卷更新日期：2019-02-18 类型：期末考试

进入出卷网下载

一、选择题

1. 布袋里有50个形状完全相同的小球，小红随机摸出一个球，记下颜色后放回摇匀，重复以上操作300次，发现摸到白色的球有61次，则布袋中白球的个数最有可能是（）

A、5个 B、10个 C、15个 D、20个

查看试题解析
2. 若反比例函数 $y = \frac{k}{x}$ 图象经过点（3，﹣1），该函数图象在（）

A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限

查看试题解析
3. 下列命题中，不正确的是（）

A、对角线相等的平行四边形是矩形 B、有一组邻边相等的四边形是菱形 C、四个角相等的四边形是矩形 D、对角线互相垂直平分且相等的四边形是正方形

查看试题解析
4. 一元二次方程 $2 x^{2} + 4 x + c = 0$ 有两个相等的实数根，那么实数 $c$ 的取值为（）

A、＞2 B、 ≥2 C、＝2 D、＝

查看试题解析
5. 四条线段 $a$ ， $b$ ， $c$ ， $d$ 成比例，其中 $b = 3 c m$ ， $c = 8 c m$ ， $d = 12 c m$ ，则 $a =$ （）

A、2㎝ B、4㎝ C、6㎝ D、8㎝

查看试题解析
6. 关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 5 x + m^{2} - 4 = 0$ 的常数项是0，则（）

A、＝4 B、＝2 C、＝2或＝-2 D、＝-2

查看试题解析
7. 已知一次函数 $y = m x + n$ 与反比例函数 $y = \frac{m}{x}$ ，其中 $m$ 、 $n$ 为常数，且 $m n$ ＜0，则它们在同一坐标系中的图象可能是（）

A、 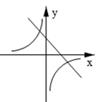B、 C、 D、

查看试题解析
8. 在平面直角坐标系中，以原点O为位似中心，把△ABC放大得到△A₁B₁C₁ ，使他们的相似比为1：2，若点A的坐标为（2，2），则它的对应点A₁的坐标一定是（）

A、（-2，-2） B、（1，1） C、（4，4） D、（4，4）或（-4，-4）

查看试题解析
9. 菱形OACB在平面直角坐标系中的位置如图所示，点C的坐标是（8，0），点A的纵坐标是2，则点B的坐标是（）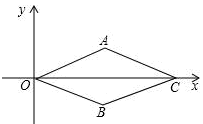

A、（4，2） B、（4，﹣2） C、（2，﹣6） D、（2，6）

查看试题解析
10. 如图所示，在矩形ABCD中，点F是 BC的中点，DF的延长线与AB的延长线相交于点E，DE与AC相交于点O，若 $S_{Δ C O D} = 2$ ，则 $S_{Δ A O E} =$ （）

A、4 B、6 C、8 D、10

查看试题解析

二、填空题

11. 已知 $\frac{x}{5} = \frac{y}{4} = \frac{z}{3}$ （x、y、z均不为零），则 $\frac{x + y}{3 y - 2 z} =$ ．

查看试题解析
12. 若 $x = 2$ 是方程 $2 x^{2} - m x - 2 = 0$ 的一个解，则 $m$ ＝．

查看试题解析
13. 小明的身高为1.6 $m$ ，他在阳光下的影长为2 $m$ ，此时他旁边的旗杆的影长为15 $m$ ，则旗杆的高度为 $m$ ．

查看试题解析
14. 菱形的周长为12，它的一个内角为60°，则菱形的较短的对角线长为．

查看试题解析
15. 双曲线 $y_{1} = \frac{4}{x}$ 、 $y_{2} = \frac{k}{x}$ 在第一象限的图象如图，过y₁上的任意一点A，作 $x$ 轴的平行线交y₂于B，交y轴于C，若 $S_{Δ A O B} = 1$ ，则 $k =$ ．

查看试题解析
16. 如图，将边长为6cm的正方形ABCD折叠，使点D落在AB边的中点E处，折痕为 FH，点C落在Q处，EQ 与BC 交于点G，则△EBG的周长是 cm．

查看试题解析

三、解答题（一）

17. 解方程： $3 x (x + 1) = 2 x + 2$

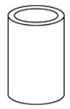
查看试题解析
18. 如图是水管的一部分（空心圆柱体），请画出它的三视图．

查看试题解析
19. 如图是一个可以自由转动的转盘，小明跟小红分别转动一次转盘，然后记下转盘停止时指针所指的颜色（指针压线时重转），若两次颜色相同则小明获胜，否则小红获胜，请你用树状图或列表的方法表示这个游戏所有可能出现的结果，并判断游戏是否公平.

查看试题解析

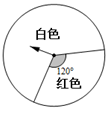
四、解答题（二）

20. 如图所示，AB平分∠CAD，∠ABC＝∠D＝90°.

(1)、求证：△ABC∽△ADB；

(2)、若AC＝6cm，AD＝4 cm，求AB的长.

查看试题解析
21. 网购已经成为一种时尚，某网络购物平台“双十一”全天交易额逐年增长，2016年交易额为500亿元，2018年交易额为720亿元。

(1)、2016年至2018年“双十一”交易额的年平均增长率是多少？

(2)、若保持原来的增长率，试计算2019年该平台“双十一”的交易额将达到多少亿元？

查看试题解析
22. 如图，等腰三角形ABC中，AB＝AC，AH⊥BC，点E是AH上一点，延长AH至点F，使FH＝EH.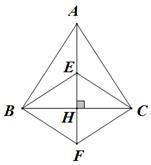

(1)、求证：四边形EBFC是菱形；

(2)、如果∠BAC＝∠ECF，求证：AC⊥CF.

查看试题解析

五、解答题（三）

23. 如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.

(1)、求证：∠DAF＝∠CDE；

(2)、求证：△ADF∽△DEC；

(3)、若AE＝6，AD＝8，AB＝7，求AF的长.

查看试题解析
24. △ABC是等边三角形，点D是射线BC上的一个动点（点D不与点B、C重合），△ADE是以AD为边的等边三角形，过点E作BC的平行线，分别交射线AB、AC于点F、G，连接BE.

(1)、如图1，当点D在线段BC上时：
①求证：△AEB≌△ADC；

②求证：四边形BCGE是平行四边形；

(2)、如图2，当点D在BC的延长线上，且CD＝BC时，试判断四边形BCGE是什么特殊的四边形？并说明理由.

查看试题解析
25. 直线 $y = k x + b$ 与反比例函数 $y = \frac{8}{x}$ （ $x$ ＞0）的图象分别交于点 A（ $m$ ，4）和点B（8， $n$ ），与坐标轴分别交于点C和点D．

(1)、求直线AB的解析式；

(2)、观察图象，当 $x > 0$ 时，直接写出 $k x + b > \frac{8}{x}$ 的解集；

(3)、若点P是 $x$ 轴上一动点，当△COD与△ADP相似时，求点P的坐标．

查看试题解析