广东省汕头市澄海区2018-2019学年八年级上学期数学期末考试试卷
试卷更新日期:2019-02-18 类型:期末考试
一、选择题
-
1. 若分式 有意义,则x的取值范围是( )A、
 B、
B、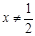 C、
C、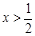 D、
D、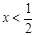 2. 下列大学的校徽图案是轴对称图形的是( )A、
2. 下列大学的校徽图案是轴对称图形的是( )A、 清华大学
B、
清华大学
B、 北京大学
C、
北京大学
C、 中国人民大学
D、
中国人民大学
D、 浙江大学
3. 下列运算正确的是( )A、
浙江大学
3. 下列运算正确的是( )A、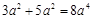 B、
B、 C、
C、 D、
D、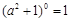 4. 若等腰三角形的周长为28cm,一边为10cm,则腰长为( )A、10cm B、9cm C、10cm或9cm D、8cm5. 一副三角板如图叠放在一起,则∠α的度数是( )
4. 若等腰三角形的周长为28cm,一边为10cm,则腰长为( )A、10cm B、9cm C、10cm或9cm D、8cm5. 一副三角板如图叠放在一起,则∠α的度数是( )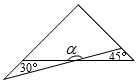
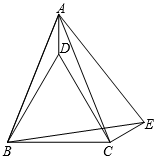
A、165° B、120° C、150° D、135°6. 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )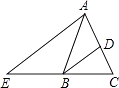 A、40° B、45° C、60° D、70°7. 计算 等于( )A、
A、40° B、45° C、60° D、70°7. 计算 等于( )A、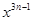 B、
B、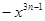 C、
C、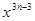 D、
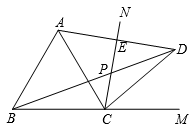
D、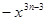 8. 如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是( )
8. 如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是( )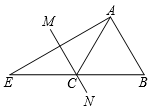 A、80° B、85° C、90° D、105°9. 已知: ,则 的值等于( )A、
A、80° B、85° C、90° D、105°9. 已知: ,则 的值等于( )A、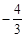 B、
B、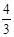 C、
C、 D、
D、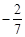 10. 如图,点P在边长为1的等边△ABC的边AB上,过点P作PE⊥AC于点E.Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
10. 如图,点P在边长为1的等边△ABC的边AB上,过点P作PE⊥AC于点E.Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( ) A、
A、 B、
C、
B、
C、 D、不能确定
D、不能确定
二、填空题
-
11. 2015年诺贝尔生理学或医学奖得主中国科学家屠呦呦,发现了一种病毒的长度约为0.00000456毫米,则数据0.00000456用科学记数法表示为 .12. 分解因式: = .13. 分式方程
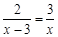 的解为 . 14. 若正 边形的每个内角都等于150°,则 的值为 .15. 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E, ,DE=2,AB=4,则AC的长是 .
的解为 . 14. 若正 边形的每个内角都等于150°,则 的值为 .15. 如图,在△ABC中,AD是∠BAC的平分线,DE⊥AB于点E, ,DE=2,AB=4,则AC的长是 .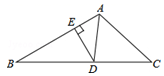 16. 已知 ,那么 的值为 .
16. 已知 ,那么 的值为 .三、解答题(一)
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 如图,已知AD,AE是△ABC的高和角平分线,∠B=44°,C=76°,求∠DAE的度数.

四、解答题(二)
-
20. 已知 , .求下列各式的值.(1)、(2)、 .21. 某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克.求第一次进价是每千克多少元?22. 下面是某同学对多项式 进行因式分解的过程.
解:设 ,则
原式=
(1)、该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果 .(2)、请你模仿以上方法尝试对多项式 进行因式分解.五、解答题(三)
-
23. 已知:在△ABC中,∠ACB=90°,点P是线段AC上一点,过点A作AB的垂线,交BP的延长线于点M,MN⊥AC于点N,PQ⊥AB于点Q,AQ=MN.
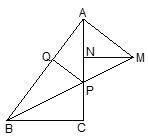
求证:
(1)、△APM是等腰三角形;(2)、PC=AN.