2017年吉林省延边州高考数学仿真试卷（理科）

试卷更新日期：2017-04-18 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合A={3a，3}，B={a²+2a，4}，A∩B={3}，则A∪B等于（）

A、{3，5} B、{3，4} C、{﹣9，3} D、{﹣9，3，4}

查看试题解析
2. 复数z满足zi=1﹣ $\sqrt{5}$ i（i为虚数单位），则z等于（）

A、﹣ $\sqrt{5}$ ﹣i B、 $\sqrt{5}$ ﹣i C、i D、﹣i

查看试题解析
3. 已知向量 $\vec{a}$ ， $\vec{b}$ ，且| $\vec{a}$ |=2 $\sqrt{3}$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{π}{6}$ ， $\vec{a}$ ⊥（3 $\vec{a}$ ﹣ $\vec{b}$ ），则| $\vec{b}$ |等于（）

A、6 B、6 $\sqrt{3}$ C、12 D、12 $\sqrt{3}$

查看试题解析
4. 等差数列{a_n}的前n项和为S_n ，且S₅=﹣15，a₂+a₅=﹣2，则公差d等于（）

A、5 B、4 C、3 D、2

查看试题解析
5.
如图所示的程序框图，运行程序后，输出的结果为（）

A、5 B、4 C、3 D、2

查看试题解析
6. 某公司在2012﹣2016年的收入与支出情况如表所示：
收入x（亿元）
2.2
2.6
4.0
5.3
5.9
支出y（亿元）
0.2
1.5
2.0
2.5
3.8
根据表中数据可得回归直线方程为 $\hat{y}$ =0.8x+ $\hat{a}$ ，依次估计如果2017年该公司收入为7亿元时的支出为（）

A、4.5亿元 B、4.4亿元 C、4.3亿元 D、4.2亿元

查看试题解析
7. 已知a=2^﹣^1.2 ， b=log₃6，c=log₅10，则a，b，c的大小关系是（）

A、c＜b＜a B、c＜a＜b C、a＜b＜c D、a＜c＜b

查看试题解析
8. 若x，y满足 ${\begin{matrix} x + y - 3 \geq 0 \\ k x - y + 3 \geq 0 \\ y \geq 0 \end{matrix}$ ，且当z=y﹣x的最小值为﹣12，则k的值为（）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、 $\frac{1}{4}$ D、﹣ $\frac{1}{4}$

查看试题解析
9. 已知一个几何体的三视图如图所示，则该几何体的体积为（）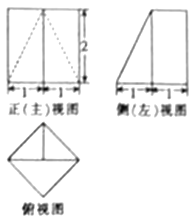

A、 $\frac{32}{3}$ B、 $\frac{16}{3}$ C、 $\frac{8}{3}$ D、 $\frac{4}{3}$

查看试题解析
10. 设函数f（x）=sin（2x+ $\frac{π}{4}$ ）（x∈[0， $\frac{8 π}{9}$ ]），若方程f（x）=a恰好有三个根，分别为x₁ ， x₂ ， x₃（x₁＜x₂＜x₃），则x₁+2x₂+x₃的值为（）

A、π B、 $\frac{3 π}{4}$ C、 $\frac{3 π}{2}$ D、 $\frac{5 π}{4}$

查看试题解析
11. 如图，在三棱柱ABC﹣A₁B₁C₁中，底面为正三角形，侧棱垂直底面，AB=4，AA₁=6，若E，F分别是棱BB₁ ， CC₁上的点，且BE=B₁E，C₁F= $\frac{1}{3}$ CC₁ ，则异面直线A₁E与AF所成角的余弦值为（）

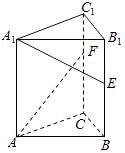A、 $\frac{\sqrt{3}}{6}$ B、 $\frac{\sqrt{2}}{6}$ C、 $\frac{\sqrt{3}}{10}$ D、 $\frac{\sqrt{2}}{10}$

查看试题解析
12. 设函数f（x）= $e^{x} (x^{3} + \frac{3}{2} x^{2} - 6 x + 2) - 2 a e^{x}$ ﹣x，若不等式f（x）≤0在[﹣2，+∞）上有解，则实数a的最小值为（）

A、 $- \frac{3}{2} - \frac{1}{e}$ B、 $- \frac{3}{2} - \frac{2}{e}$ C、 $- \frac{3}{4} - \frac{1}{2 e}$ D、 $- 1 - \frac{1}{e}$

查看试题解析

二、填空题

13. 若（1﹣2x）⁵=a₀+a₁x+a₂x²+a₃x³+a₄x⁴+a₅x⁵ ，则 $\frac{a_{3}}{a_{2}}$ = ．

查看试题解析
14. 设等比数列{a_n}的前n项和为S_n ，若a₃=2a₄=2，则S₆= ．

查看试题解析
15. 我国古代数学著作《九章算术》有如下问题：“今有人持金出五关，前关二而税一，次关三而税一，次关四而税一，次关五而税一，次关六而税一，并五关所税，适重一斤，问本持金几何”其意思为“今有人持金出五关，第1关收税金 $\frac{1}{2}$ ，第2关收税金为剩余金的 $\frac{1}{3}$ ，第3关收税金为剩余金的 $\frac{1}{4}$ ，第4关收税金为剩余金的 $\frac{1}{5}$ ，第5关收税金为剩余金的 $\frac{1}{6}$ ，5关所收税金之和，恰好重1斤，问原来持金多少？”若将题中“5关所收税金之和，恰好重1斤，问原来持金多少？”改成假设这个原来持金为x，按此规律通过第8关，则第8关需收税金为x．

查看试题解析
16. 已知抛物线y= $\frac{1}{16}$ x² ， A，B是该抛物线上两点，且|AB|=24，则线段AB的中点P离x轴最近时点的纵坐标为．

查看试题解析

三、解答题

17. 设△ABC的内角A，B，C的对边分别为a，b，c，若c=2 $\sqrt{3}$ ，sinB=2sinA．

(1)、若C= $\frac{π}{3}$ ，求a，b的值；

(2)、若cosC= $\frac{1}{4}$ ，求△ABC的面积．

查看试题解析
18. 如图，在棱柱ABC﹣A₁B₁C₁中，点C在平面A₁B₁C₁内的射影点为的A₁B₁中点O，AC=BC=AA₁ ， ∠ACB=90°．

(1)、求证：AB⊥平面OCC₁；

(2)、求二面角A﹣CC₁﹣B的正弦值．

查看试题解析
19. 近年来我国电子商务行业迎来蓬勃发展新机遇，2016年双11期间，某网络购物平台推销了A，B，C三种商品，某网购者决定抢购这三种商品，假设该名网购者都参与了A，B，C三种商品的抢购，抢购成功与否相互独立，且不重复抢购同一种商品，对A，B，C三件商品抢购成功的概率分别为a，b， $\frac{1}{4} (a > b)$ ，已知三件商品都被抢购成功的概率为 $\frac{1}{24}$ ，至少有一件商品被抢购成功的概率为 $\frac{3}{4}$ ．

(1)、求a，b的值；

(2)、若购物平台准备对抢购成功的A，B，C三件商品进行优惠减免，A商品抢购成功减免2百元，B商品抢购成功减免4比百元，C商品抢购成功减免6百元．求该名网购者获得减免总金额（单位：百元）的分别列和数学期望．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}}$ + $\frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右焦点分别为F₁、F₂ ，由椭圆短轴的一个端点与两个焦点构成一个等边三角形．它的面积为4 $\sqrt{3}$ ．

(1)、求椭圆C的方程；

(2)、已知动点B（m，n）（mn≠0）在椭圆上，点A（0，2 $\sqrt{3}$ ），直线AB交x轴于点D，点B′为点B关于x轴的对称点，直线AB′交x轴于点E，若在y轴上存在点G（0，t），使得∠OGD=∠OEG，求点G的坐标．

查看试题解析
21. 已知函数f（x）=2lnx﹣3x²﹣11x．

(1)、求曲线y=f（x）在点（1，f（1））处的切线方程；

(2)、若关于x的不等式f（x）≤（a﹣3）x²+（2a﹣13）x+1恒成立，求整数a的最小值．

查看试题解析
22. [选修4-4：坐标系与参数方程选讲]

已知曲线C₁的极坐标方程为ρ²cos2θ=8，曲线C₂的极坐标方程为 $θ = \frac{π}{6}$ ，曲线C₁、C₂相交于A、B两点．
（Ⅰ）求A、B两点的极坐标；
（Ⅱ）曲线C₁与直线 ${\begin{matrix} x = 2 + \frac{\sqrt{3}}{2} t \\ y = \frac{1}{2} t \end{matrix}$ （t为参数）分别相交于M，N两点，求线段MN的长度．

查看试题解析
23. [选修4-5：不等式选讲]

已知函数f（x）=|2x﹣a|+a．

(1)、当a=3时，求不等式f（x）≤6的解集；

(2)、设函数g（x）=|2x﹣3|，∀x∈R，f（x）+g（x）≥5，求a的取值范围．

查看试题解析

收入x（亿元）	2.2	2.6	4.0	5.3	5.9
支出y（亿元）	0.2	1.5	2.0	2.5	3.8