2018-2019学年初中数学华师大版九年级下册28.3借助调查作决策 同步练习
试卷更新日期：2019-02-16 类型：同步测试
一、选择题
-
1. 如图是交警在一个路口统计的某个时段来往车辆的车速（单位：千米/时）情况．则这些车的车速的众数、中位数分别是（ ）
A、8，6 B、8，5 C、52，53 D、52，522.如图是某班45名同学爱心捐款额的频数分布直方图（每组含前一个边界值，不含后一个边界值），则捐款人数最多的一组是（ ）
A、5～10元 B、10～15元 C、15～20元 D、20～25元3.如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图（两图都不完整），下列结论错误的是（ ）
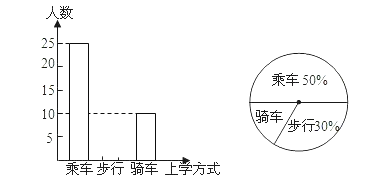A、该班总人数为50人 B、步行人数为30人 C、乘车人数是骑车人数的2.5倍 D、骑车人数占20%4. 某校对初三年级1600名男生的身高进行了测量，结果身高（单位：m）在1.58～1.65这一小组的频率为0.4，则该组的人数为（ ）A、640人 B、480 人 C、400人 D、40人5. 某校组织400名九年级学生参加英语测试，为了解他们的测试情况（满分120分），随机抽取若干名学生，将所得成绩数据整理后，画出频数分布直方图（如图）．估计该校成绩在100～120分之间的人数有（ ）
A、12 B、48 C、60 D、726.为了解在校学生参加课外兴趣小组活动情况，随机调查了40名学生，将结果绘制成了如图所示的频数分布直方图，则参加书法兴趣小组的频率是（ ）
A、0.1 B、0.15 C、0.2 D、0.37.为了了解本校九年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25～30次的频率是（ ）
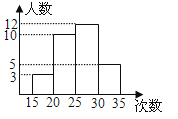A、0.1 B、0.2 C、0.3 D、0.48. 某人在调查了本班同学的体重情况后，画出了频数分布图如图．下列结论中，不正确的是（ ）
A、全班总人数40人 B、学生体重的众数是13 C、学生体重的中位数落在50～55千克这一组 D、体重在60～65千克的人数占全班总人数的
二、填空题
-
9. 已知在一个样本中，50个数据分别落在5个组内，第一，二，三，四，五组数据的个数分别是2，8，15，20，5，则第四组频数为 ．10. 在全国初中数学竞赛中，都匀市有40名同学进入复赛，把他们的成绩分为六组，第一组一第四组的人数分别为10，5，7，6，第五组的频率是0.2，则第六组的频率是 ．11.
某记者抽样调查了某校一些学生假期用于读书的时间（单位：分钟）后，绘制了频数分布直方图，从左到右的前5个长方形相对应的频率之和为0.9，最后一组的频数是15，则此次抽样调查的人数为 人．（注：横轴上每组数据包含最小值不包含最大值）
12. 为了解某校九年级女生1分钟仰卧起坐的次数，从中随机抽查了50名女生参加测试，被抽查的女生中有90%的女生次数不小于30次，并绘制成频数分布直方图（如图），那么仰卧起坐的次数在40～45的频率是 ．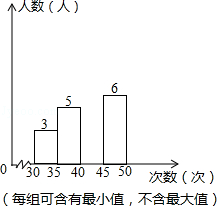
13.某区在初一年级一次数学期末考试后，随机抽查了部分同学的成绩，整理成频数分布直方图如图，则本次抽查的样本的中位数所在的区间是
14.根据去年某班学生体育毕业考试的成绩（成绩取整数），制成如图所示的频数分布直方图，若成绩在24.5～27.5分范围内为良好，则该班学生体育成绩良好的百分率是 ．
三、解答题
-
15. 我市某校在推进新课改的过程中，开设的体育选修课有：A：篮球，B：足球，C：排球，D：羽毛球，E：乒乓球，学生可根据自己的爱好选修一门，学校李老师对某班全班同学的选课情况进行调查统计，制成了两幅不完整的统计图（如图）．
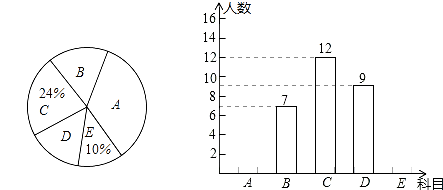(1)、请你求出该班的总人数，并补全频数分布直方图；(2)、该班班委4人中，1人选修篮球，2人选修足球，1人选修排球，李老师要从这4人中人任选2人了解他们对体育选课的看法，请你用列表或画树状图的方法，求选出的2人恰好1人选修篮球，1人选修足球的概率．16. 九年级（1）班开展了为期一周的“敬老爱亲”社会活动，并根据学生做家务的时间来评价他们在活动中的表现，老师调查了全班50名学生在这次活动中做家务的时间，并将统计的时间（单位：小时）分成5组：A.0.5≤x＜1 B.1≤x＜1.5 C.1.5≤x＜2 D.2≤x＜2.5 E.2.5≤x＜3；并制成两幅不完整的统计图（如图）：
请根据图中提供的信息，解答下列问题：
(1)、这次活动中学生做家务时间的中位数所在的组是；(2)、补全频数分布直方图；(3)、该班的小明同学这一周做家务2小时，他认为自己做家务的时间比班里一半以上的同学多，你认为小明的判断符合实际吗？请用适当的统计知识说明理由．17. 为了了解1200名学生对学校设置的体操、篮球、足球、跑步、舞蹈等课外体育活动项目的喜爱情况，在全校范围内随机抽取了若干名学生．对他们最喜爱的体育项目（每人只选一项）进行了问卷调查，将数据进行了统计并绘制成了如图的频数分布直方图和扇形统计图（均不完整）．
(1)、在这次问卷调查中，一共抽查了名学生；(2)、估计该校1200名学生中有人最喜爱篮球活动；(3)、补全频数分布直方图．18. 某外国语学校组织九年级学生参加数、科、英竞赛培训，下面两幅统计图反映了学生自愿报名（每人限报一科）的情况，请你根据图中信息回答下列问题：
(1)、九年级报名参加参加三科培训的总人数是 ．(2)、英语学科所在扇形圆心角的度数是 ， 请补全上述统计图．(3)、根据实际情况，需从英语组抽调部分同学到数学组，使数学组人数是英语组人数的3倍，则应从英语组抽调多少名学生？19. 中小学生的视力状况越来越受到全社会的广泛关注．某市有关部门对全市5万名初中生的视力情况进行了一次抽样调查，统计人员利用所得数据绘制的尚不完整的扇形统计图（图1）和频数分布直方图（图2）（长方形的高表示该组人数），根据图中所提供的信息回答下列问题；
(1)、本次调查共抽测了多少名学生；(2)、补全图2的频数分布直方图；(3)、在扇形统计图（图1）中，视力在5.2～5.5所在扇形占的百分比为多少；(4)、在这个问题中的样本指的是什么；(5)、求全市有多少名初中生的视力在4.9～5.2（含4.9，不含5.2）范围内．20. 某中学为了预测本校应届毕业生“一分钟跳绳”项目的考试情况，从九年级随机抽取部分女生进行该项目测试，并以测试数据为样本，绘制出如图1的部分频数分布直方图（从左到右依次为六个小组，每小组含最小值，不含最大值）和图2扇形统计图．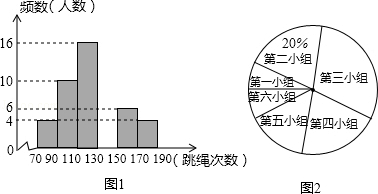
根据统计图提供的信息解答下列问题：
(1)、补全图1频数分布直方图，并指出这个样本数据的中位数落在第小组；(2)、若“一分钟跳绳”不低于130次的成绩为优秀，本校九年级女生共有260人，请估计该校九年级女生“一分钟跳绳”成绩的优秀人数；(3)、若“一分钟跳绳”成绩不低于170次的为满分，不低于130次的为优秀，在这个样本中，从成绩为优秀的女生中任选一人，她的成绩为满分的概率是多少？21. 在某班的一次数学考试中，满分为150分，学生得分全为整数，将全班学生成绩从75到150依次分为5组，统计数据如图1．
(1)、该班共有名学生，将图1补充完整；(2)、从图2中，第四组的圆心角度数为°(3)、从这个班中随机抽取一名学生，求该生恰属于第二组的概率．22. 行人过路口不走人行横道或者过街设施、车辆行人闯红灯、酒后驾驶、违法停车、飙车、违反禁令标志、违法使用公交专用道、违法穿插排队车辆等是八类严重影响城市交通秩序的交通违法行为．为了配合某市公安机关整治城市交通秩序集中统一行动启动．小明和他的同学在城区中心的一个十字路口，观察、统计白天抽取几个时段中闯红灯的人次．制作了如下的两个数据统计图，其中老年人闯红灯人次为18人．
(1)、统计的时段内，闯红灯一共为多少人次？(2)、求图1提供的五个数据（各时段闯红灯人次）的中位数，并补全条形图；(3)、估计一个月（按30天计算）白天统计时段，在该十字路口闯红灯的未成年人约有多少人次？23. 为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等等课外体育活动项目的喜爱情况，在全校范围内随机抽取了若干名学生．对他们最喜爱的体育项目（每人只选一项）进行了问卷调查，将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图（均不完整）．
(1)、在这次问卷调查中，一共抽查了多少名学生？(2)、补全频数分布直方图；(3)、估计该校1800名学生中有多少人最喜爱球类活动？