2018-2019学年初中数学华师大版九年级下册28.2 用样本估计总体 同步练习
试卷更新日期：2019-02-16 类型：同步测试
一、选择题
-
1. 下列抽样方法是随机抽样的是（ ）A、为了解刚生产的零件的质量情况，从每一个包装箱内抽5个加以检查 B、为了解全市学生的身高情况，以一、三中的学生为代表进行考察 C、为了解小学生的视力情况，选中六年级20名学生进行调查 D、为了解某地区的车流量，记录某一红绿灯处早上8：00至9：00的车流量2. 为了了解某中学(共有3个年级，每年级6个班)学生完成作业情况，可采用下列方式进行调查：①向3个年级每个班级的班长做调查；②向3个年级每个班的学习委员做调查；③向各班级每班前10名学生做调查；④将18个班级编号，从中任意抽取3个班级，向这3个班级的所有学生做调查．你认为调查具有随机性的是（ ）A、① B、② C、③ D、④3. 随机抽样不具有的性质是（ ）A、抽得的样本具有随机性 B、抽得的样本具有代表性 C、抽得的样本具有广泛性 D、抽得的样本具有偏向性4. 下列表述不正确的是（ ）A、样本选取不当时，用样本估计总体不可靠 B、有的较小的样本的平均数和标准差与总体的平均数和标准差差距也不大 C、有的较大的样本的平均数和标准差与总体的平均数和标准差差距也不小 D、选取的样本容量越大，这种抽样调查的方法越科学5. 一池塘中大约有鱼苗数为50 000尾，为了解池塘中鱼苗的长势，现需从中捞取一些鱼苗进行抽样调查，那么捞出鱼苗数最合适的是（ ）A、1尾 B、50尾 C、500尾 D、1 000尾6. 某社会调查队对城区一个社区居民的家庭经济状况进行调查．调查的结果是：该社区共有500户，高收入、中等收入和低收入家庭分别有125户、280户和95户．已知该市有100万户家庭，下列表述正确的是（ ）A、该市高收入家庭约25万户 B、该市中等收入家庭约56万户 C、该市低收入家庭约19万户 D、因为城市社区家庭的经济状况较好，所以不能据此数据估计全市所有家庭的经济状况7. 某环保网站正在对商店使用环保购物袋程度进行在线调查，以这个调查来作为居民支持商店使用环保购物袋程度的估计是（ ）A、合理的 B、不能确定 C、不合理的 D、以上都不对8. 下列调查方式的选择正确的是（ ）A、为了解青年人的体质状况，选择运动员进行调查 B、为了解全市老年人的健康状况，选择公园中散步的老人进行调查 C、为了解某省所有家庭的用电情况，随机抽查某个小区所有家庭的用电情况 D、为了解10箱某种汽水的质量，随机抽取10瓶进行鉴定9. 在对300名学生考试成绩用简单随机抽样方式进行抽样调查时，第一次从盒子中抽出表示一个编号的纸条，那么，在抽下一个表示编号的纸条之前，他已抽出的这个纸条放入盒子是（ ）A、应当的 B、不应当的 C、没有影响 D、以上都不对
二、填空题
-
10. 小刚想产生3个0～6的随机整数，但手头没有产生随机数的计算器，如果恰好有一枚普通的正方体骰子，那么他可以采取的方法是 ．11. 对九年级学生进行健康状况调查．方案是按照每位学生的学号取12，42，72，102，132，162……这样的抽样调查 简单的随机抽样．(填“是”或“不是”)12. 一般来说，要了解一个城市的空气污染情况，观察一个月得到的结论可靠，还是春、夏、秋、冬各观察一个月得到的结论可靠？13. 用在高速公路上行驶的汽车耗油1L所行走的路程来估计1L汽油能使汽车行走多少路程的试验中，样本的选取 ． （填“可靠”或“不可靠”）
三、解答题
-
14. 兰州市某中学对本校初中学生完成家庭作业的时间做了总量控制，规定每天完成家庭作业的时间不超过1.5小时，该校数学课外兴趣小组对本校初中学生回家完成作业的时间做了一次随机抽样调查，并绘制出频数分布表和频数分布直方图的一部分．
时间(小时)
频数(人数)
频率
0≤t＜0.5
4
0.1
0.5≤t＜1
a
0.3
1≤t＜1.5
10
0.25
1.5≤t＜2
8
b
2≤t＜2.5
6
0.15
合计
1
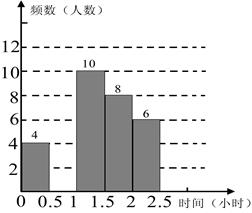(1)、在表中，a＝ ， b＝；(2)、补全频数分布直方图；(3)、请估计该校1 400名初中学生中，约有多少学生在1.5小时以内完成了家庭作业．15. 期中考试后，数学课代表小丽在计算全班50名同学数学平均成绩时，按简单随机抽样法抽出10名同学的学号．(1)、这10名同学的成绩为全班最好，如此巧合的抽样有可能吗？假如我们用这10个样本的平均数估计全班同学的数学成绩，将会得出怎样的结果？能否代表全班同学数学学习水平？(2)、使用简单随机抽样的方法，既然有可能存在如（1）那样的巧合：抽到全班成绩最高的10名同学的分数作为样本，当然也有可能抽到恰为全班成绩较低的10名同学的分数作为样本，于是小丽提出了质疑“简单随机抽样方法不可靠”．你的看法如何？