2018-2019学年初中数学华师大版九年级下册第二十七章《圆》章末测试
试卷更新日期:2019-02-16 类型:单元试卷
一、选择题
-
1. 如图,BC是⊙O的直径,AD⊥BC,若∠D=36°.则∠BAD的度数是( )
 A、72° B、54° C、45° D、36°2. 将 沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( )
A、72° B、54° C、45° D、36°2. 将 沿弦BC折叠,交直径AB于点D,若AD=4,DB=5,则BC的长是( ) A、3 B、8 C、 D、23. 如图,AB是⊙O的直径,点C,D在⊙O上,且点C、D在AB的异侧,连结AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
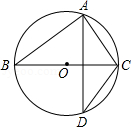
A、3 B、8 C、 D、23. 如图,AB是⊙O的直径,点C,D在⊙O上,且点C、D在AB的异侧,连结AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )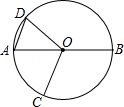 A、70° B、60° C、50° D、40°4. 如图,等圆⊙O1和⊙O2相交于A,B两点,⊙O1经过⊙O2的圆心O2 , 连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( )
A、70° B、60° C、50° D、40°4. 如图,等圆⊙O1和⊙O2相交于A,B两点,⊙O1经过⊙O2的圆心O2 , 连接AO1并延长交⊙O1于点C,则∠ACO2的度数为( ) A、60° B、45° C、30° D、20°5. 关于半径为5的圆,下列说法正确的是( )A、若有一点到圆心的距离为5,则该点在圆外 B、若有一点在圆外,则该点到圆心的距离不小于5 C、圆上任意两点之间的线段长度不大于10 D、圆上任意两点之间的部分可以大于10π6. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,联结BC,若∠A=36°,则∠C等于( )
A、60° B、45° C、30° D、20°5. 关于半径为5的圆,下列说法正确的是( )A、若有一点到圆心的距离为5,则该点在圆外 B、若有一点在圆外,则该点到圆心的距离不小于5 C、圆上任意两点之间的线段长度不大于10 D、圆上任意两点之间的部分可以大于10π6. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,联结BC,若∠A=36°,则∠C等于( )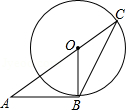 A、36° B、54° C、60° D、27°7. 如图,PA与⊙O相切于点A,PO的延长线与⊙O交于点C,若⊙O的半径为3,PA=4.弦AC的长为( )
A、36° B、54° C、60° D、27°7. 如图,PA与⊙O相切于点A,PO的延长线与⊙O交于点C,若⊙O的半径为3,PA=4.弦AC的长为( ) A、5 B、
A、5 B、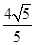 C、
C、 D、
D、 8. 如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )
8. 如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( ) A、 B、π C、2π D、4π
A、 B、π C、2π D、4π二、填空题
-
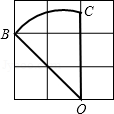
9. 在边长为1的3×3的方格中,点B、O都在格点上,则劣弧BC的长是 .
 10. 已知扇形弧长为2π,半径为3cm,则此扇形所对的圆心角为度.11. 已知⊙A的半径为5,圆心A(3,4),坐标原点O与⊙A的位置关系是 .12.
10. 已知扇形弧长为2π,半径为3cm,则此扇形所对的圆心角为度.11. 已知⊙A的半径为5,圆心A(3,4),坐标原点O与⊙A的位置关系是 .12.如图,⊙O的半径OC=5cm , 直线l⊥OC , 垂足为H , 且l交⊙O于A、B两点,AB=8cm , 则l沿OC所在直线向下平移 cm时与⊙O相切.
 13. 如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为 cm.
13. 如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为 cm. 14. 如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,CH=1cm,则AB=cm.
14. 如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,CH=1cm,则AB=cm.
三、解答题
-
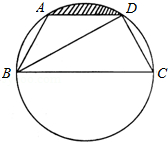
15. 如图,点A、B、C、D在⊙O上,∠ADC=60°,C是弧AB的中点.
 (1)、判断△ABC的形状,并说明理由;(2)、若BC=6 cm,求图中阴影部分的面积.16. 如图,在△ABC中,AB=AC,AD为△ABC的高,以AD为直径的⊙0与AB、AC两边分别交于点E、F.连接DE、DF.
(1)、判断△ABC的形状,并说明理由;(2)、若BC=6 cm,求图中阴影部分的面积.16. 如图,在△ABC中,AB=AC,AD为△ABC的高,以AD为直径的⊙0与AB、AC两边分别交于点E、F.连接DE、DF. (1)、求证:BE=CF;(2)、若AD=BC=2 .求ED的长.17. 如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E.
(1)、求证:BE=CF;(2)、若AD=BC=2 .求ED的长.17. 如图,已知在△ABC中,AB=AC,D是△ABC外接圆劣弧AC上的点(不与A,C重合),延长BD至E. (1)、求证:AD的延长线平分∠CDE;(2)、若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.18. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)、求证:AD的延长线平分∠CDE;(2)、若∠BAC=30°,且△ABC底边BC边上高为1,求△ABC外接圆的周长.18. 如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD (1)、求证:BD平分∠ABC;(2)、当∠ODB=30°时,求证:BC=OD.19. 如图,AC是⊙O的直径,弦BD交AC于点E.
(1)、求证:BD平分∠ABC;(2)、当∠ODB=30°时,求证:BC=OD.19. 如图,AC是⊙O的直径,弦BD交AC于点E.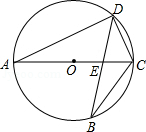 (1)、求证:△ADE∽△BCE;(2)、如果AD2=AE•AC,求证:CD=CB.20. 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E.
(1)、求证:△ADE∽△BCE;(2)、如果AD2=AE•AC,求证:CD=CB.20. 如图,以AB为直径的⊙O交∠BAD的角平分线于C,过C作CD⊥AD于D,交AB的延长线于E. (1)、求证:CD为⊙O的切线.(2)、若 = ,求cos∠DAB.21. 如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,CE=CF,连结AF和BE,点O在BE上,⊙O经过点B、F,交BE于点G.
(1)、求证:CD为⊙O的切线.(2)、若 = ,求cos∠DAB.21. 如图,AC=BC,∠C=90°,点E在AC上,点F在BC上,CE=CF,连结AF和BE,点O在BE上,⊙O经过点B、F,交BE于点G. (1)、求证:△ACF≌△BCE;(2)、求证:AF是⊙O的切线.
(1)、求证:△ACF≌△BCE;(2)、求证:AF是⊙O的切线.