2018-2019学年初中数学华师大版九年级下册27.1.2圆的对称性（2）同步练习
试卷更新日期：2019-02-16 类型：同步测试
一、选择题
-
1. 如图，直线l1∥l2 ， 点A在直线l1上，以点A为圆心，适当长为半径画弧，分别交直线l1、l2于B、C两点，连接AC、BC．若∠ABC=54°，则∠1的大小为（ ）
A、36° B、54° C、72° D、73°2. CD是⊙O的一条弦，作直径AB，使AB⊥CD，垂足为E，若AB=10，CD=8，则BE的长是（ ）
A、8 B、2 C、2或8 D、3或73. 如图，圆心在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A（0，1），过点P（0，﹣7）的直线l与⊙B相交于C，D两点．则弦CD长的所有可能的整数值有（ ）A、1个 B、2个 C、3个 D、4个4. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以点C为圆心，CA为半径的圆与AB交于点D，则AD的长为（ ）
A、
B、
C、
D、
5. 小英家的圆形镜子被打碎了，她拿了如图（网格中的每个小正方形边长为1）的一块碎片到玻璃店，配制成形状、大小与原来一致的镜面，则这个镜面的半径是（ ）
A、2 B、 C、 2 D、36. 在圆柱形油槽内装有一些油．截面如图，油面宽AB为6分米，如果再注入一些油后，油面AB上升1分米，油面宽变为8分米，圆柱形油槽直径MN为（ ）
A、6分米 B、8分米 C、10分米 D、12分米7. 如图所示，在⊙O中， ，∠A=30°，则∠B=（ ）
A、150° B、75° C、60° D、15°8. 如图，已知⊙O的两条弦AC，BD相交于点E，∠A=70°，∠c=50°，那么sin∠AEB的值为（ ）
A、
B、
C、
D、
二、填空题
-
9. 如图，⊙O的半径为1cm，弦AB、CD的长度分别为 cm，1cm，则弦AC、BD所夹的锐角α=度．
10. 如图，一个宽为2厘米的刻度尺（刻度单位：厘米），放在圆形玻璃杯的杯口上，刻度尺的一边与杯口外沿相切，另一边与杯口外沿两个交点处的读数恰好是3和9，那么玻璃杯的杯口外沿半径为厘米．
11. 工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小圆孔的宽口AB的长度为mm．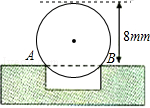
12. 如图，将⊙O沿弦AB折叠，使 经过圆心O，则∠OAB= ．
13. 如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=18°，则∠AOC的度数为度．
14. 如图，正方形ABCD的边长为2，E、F、G、H分别为各边中点，EG、FH相交于点O，以O为圆心，OE为半径画圆，则图中阴影部分的面积为 ．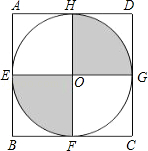
三、解答题
-
15. 如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径．
16. 如图，在同一平面内，有一组平行线l1、l2、l3 ， 相邻两条平行线之间的距离均为4，点O在直线l1上，⊙O与直线l3的交点为A、B，AB=12，求⊙O的半径．
17. 如图，⊙O的半径为17cm，弦AB∥CD，AB=30cm，CD=16cm，圆心O位于AB，CD的上方，求AB和CD的距离.
18. 机器人“海宝”在某圆形区域表演“按指令行走”，如图所示，“海宝”从圆心O出发，先沿北偏西67.4°方向行走13米至点A处，再沿正南方向行走14米至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上．
(1)、求弦BC的长；(2)、求圆O的半径长．（本题参考数据：sin67.4°= ，cos67.4°= ，tan67.4°= ）19. 如图，平面直角坐标系中，以点C（2， ）为圆心，以2为半径的圆与x轴交于A，B两点．
(1)、求A，B两点的坐标；(2)、若二次函数y=x2+bx+c的图象经过点A，B，试确定此二次函数的解析式．20. 如图，是一个匀速旋转（指每分钟旋转的弧长或圆心角相同）的摩天轮的示意图，O为圆心，AB为水平地面，假设摩天轮的直径为80米，最低点C离地面为6米，旋转一周所用的时间为6分钟，小明从点C乘坐摩天轮（身高忽略不计），请问：
(1)、经过2分钟后，小明离开地面的高度大约是多少米？(2)、若小明到了最高点，在视线没有阻挡的情况下能看到周围3公里远的地面景物，则他看到的地面景物有多大面积？（精确到1平方公里）21. 如图，台风中心位于点P，并沿东北方向PQ移动，已知台风移动的速度为40千米/时，受影响区域的半径为260千米，B市位于点P的北偏东75°方向上，距离P点480千米．
(1)、说明本次台风是否会影响B市；(2)、若这次台风会影响B市，求B市受台风影响的时间．
