2018-2019学年初中数学华师大版九年级下册27.1.2圆的对称性(1)同步练习
试卷更新日期:2019-02-16 类型:同步测试
一、选择题
-
1. 在同圆或等圆中,下列说法错误的是( )A、相等弦所对的弧相等 B、相等弦所对的圆心角相等 C、相等圆心角所对的弧相等 D、相等圆心角所对的弦相等2. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
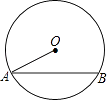 A、6 B、5 C、4 D、33. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、 cm B、
A、6 B、5 C、4 D、33. 已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A、 cm B、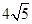 cm
C、 cm或
cm
C、 cm或 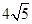 cm
D、 cm或 cm
4. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( )
cm
D、 cm或 cm
4. 如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为( ) A、2 B、4 C、6 D、85. 如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( )
A、2 B、4 C、6 D、85. 如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是( ) A、AE=BE B、
A、AE=BE B、 =
C、OE=DE
D、∠DBC=90°
6. 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )
=
C、OE=DE
D、∠DBC=90°
6. 如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为 ,则a的值是( )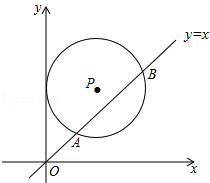 A、4 B、
A、4 B、 C、
D、
C、
D、 7. 已知⊙O的面积为2π,则其内接正三角形的面积为( )A、3 B、3 C、 D、
7. 已知⊙O的面积为2π,则其内接正三角形的面积为( )A、3 B、3 C、 D、 8. 如图,半径为3的⊙O内有一点A,OA= ,点P在⊙O上,当∠OPA最大时,PA的长等于( )
8. 如图,半径为3的⊙O内有一点A,OA= ,点P在⊙O上,当∠OPA最大时,PA的长等于( ) A、 B、 C、3 D、2
A、 B、 C、3 D、2二、填空题
-
9. 如图,已知直线AB与⊙O相交于A、B两点,∠OAB=30°,半径OA=2,那么弦AB= .
 10. 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是
10. 如图,⊙O的半径是5,AB是⊙O的直径,弦CD⊥AB,垂足为P,若CD=8,则△ACD的面积是 11. 如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
11. 如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 . 12. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm.
12. 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2 cm,∠BCD=22°30′,则⊙O的半径为cm.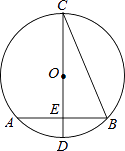 13. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 .
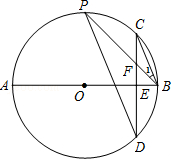
13. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是 . 14. 如图,AB是⊙O的直径,BC是弦,点E是 的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 .
14. 如图,AB是⊙O的直径,BC是弦,点E是 的中点,OE交BC于点D.连接AC,若BC=6,DE=1,则AC的长为 .
三、解答题
-
15. 如图,AB是⊙O的弦,点C、D在弦AB上,且AD=BC,联结OC、OD.求证:△OCD是等腰三角形.
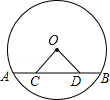 16. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
16. 已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).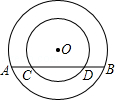 (1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.17. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
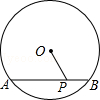
(1)、求证:AC=BD;(2)、若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.17. 如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB. (1)、若CD=16,BE=4,求⊙O的直径;(2)、若∠M=∠D,求∠D的度数.18. 如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
(1)、若CD=16,BE=4,求⊙O的直径;(2)、若∠M=∠D,求∠D的度数.18. 如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.