2018-2019学年初中数学华师大版八年级下册17.3.3 一次函数的性质 同步练习
试卷更新日期:2019-02-16 类型:同步测试
一、选择题
-
1. 正比例函数 y=(k-2)x 中,y 随 x 的增大而减小,则 k 的取值范围是( )A、k≥2 B、k≤2 C、k>2 D、k<22. 若一次函数 的函数值 随 的增大而减小,且图象与 轴的负半轴相交,那么对 和 的符号判断正确的是( )A、
 ,
,  B、
B、 ,
,  C、
C、 ,
,  D、
D、 ,
,  3. 已知两个一次函数 , 的图象相互平行,它们的部分自变量与相应的函数值如下表:
3. 已知两个一次函数 , 的图象相互平行,它们的部分自变量与相应的函数值如下表:则m的值是( )
 A、 B、 C、
A、 B、 C、 D、
4. 已知(-1,y1),(1.8,y2),(- , y3)是直线 y = -3x + m (m 为常数)上的三个点,则 y1 , y2 , y3的大小关系是( )A、y3>y1>y2 B、y1>y3>y2 C、y1>y2>y3 D、y3>y2>y15. 当x>0时,四个函数 y=—x ,y=2x+1, , ,其中y随x的增大而增大的函数有( )A、1个 B、2个 C、3个 D、4个6. 一次函数y=kx+b,当k>0,b<0时,它的图象是( )A、
D、
4. 已知(-1,y1),(1.8,y2),(- , y3)是直线 y = -3x + m (m 为常数)上的三个点,则 y1 , y2 , y3的大小关系是( )A、y3>y1>y2 B、y1>y3>y2 C、y1>y2>y3 D、y3>y2>y15. 当x>0时,四个函数 y=—x ,y=2x+1, , ,其中y随x的增大而增大的函数有( )A、1个 B、2个 C、3个 D、4个6. 一次函数y=kx+b,当k>0,b<0时,它的图象是( )A、 B、
B、 C、
C、 D、
D、 7. 定义:给定关于 的函数 ,对于该函数图象上任意两点 , ,当 时,都有 为增函数. 根据以上定义,可以判断下面所给的函数中:① ;② ;③ ;④ .是增函数的有( )A、①② B、①③ C、①④ D、③④8. 关于直线 ,下列说法不正确的是( )A、 点
7. 定义:给定关于 的函数 ,对于该函数图象上任意两点 , ,当 时,都有 为增函数. 根据以上定义,可以判断下面所给的函数中:① ;② ;③ ;④ .是增函数的有( )A、①② B、①③ C、①④ D、③④8. 关于直线 ,下列说法不正确的是( )A、 点 在
在  上
B、
上
B、 经过定点
经过定点 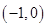 C、 当
C、 当  时,
时,  随
随  的增大而增大
D、
的增大而增大
D、 经过第一、二、三象限
9. 正比例函数图象y=(1-m)x的图像经过第一,三象限,则m的取值范围是( )A、m=1 B、m>1 C、m<1 D、m≥110. 已知P1(-3,y1),P2(2,y2)是一次函数y=2x-b的图象上的两个点,则y1,y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定
经过第一、二、三象限
9. 正比例函数图象y=(1-m)x的图像经过第一,三象限,则m的取值范围是( )A、m=1 B、m>1 C、m<1 D、m≥110. 已知P1(-3,y1),P2(2,y2)是一次函数y=2x-b的图象上的两个点,则y1,y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定二、填空题
-
11. 一次函数 与 轴交于点 , 与 轴交于点 , 随 的增大而.12. 已知一次函数y=(2﹣m)x+2的图象上两点A(x1 , y1),B(x2 , y2),当x1<x2时,有y1>y2 , 那么m的取值范围是 .13. 若点P(-3, ),Q(2, )在一次函数 的图象上,则 与 的大小关系是14. 一次函数y=kx+b,当1≤x≤4时,3≤y≤6,则 的值是 .15. 在一次函数y=kx+2中,若y随x的增大而增大,则k0.(填“>”或“<”) ,它的图象不经过第象限.16. 已知函数 的图像过点(0,-1)和(-1,1),且点 和点 都在这个函数图象上,则 的大小关系是
三、解答题
-
17. 已知一次函数 的图象与y轴交点在x轴上方,且y随x的增大而减小,求m的取值范围.18. 已知一次函数 .
 (1)、求图象与两条坐标轴的交点坐标,并在下面的直角坐标系中画出它的图象;(2)、从图象看, 随着 的增大而增大,还是随 的增大而减小?(3)、 取何值时, ?19. 已知一次函数y=kx+b的图象如图所示.
(1)、求图象与两条坐标轴的交点坐标,并在下面的直角坐标系中画出它的图象;(2)、从图象看, 随着 的增大而增大,还是随 的增大而减小?(3)、 取何值时, ?19. 已知一次函数y=kx+b的图象如图所示. (1)、确定k、b的符号;(2)、若点(﹣1,p),(2,t)在函数图象上,比较p、t的大小.20. 已知正比例函数y=kx图象经过点(3,-6),求:(1)、这个函数的解析式;(2)、判断点A(4,-2)是否在这个函数图象上.
(1)、确定k、b的符号;(2)、若点(﹣1,p),(2,t)在函数图象上,比较p、t的大小.20. 已知正比例函数y=kx图象经过点(3,-6),求:(1)、这个函数的解析式;(2)、判断点A(4,-2)是否在这个函数图象上.
(3)、图象上的两点B(x1 , y1)、C(x2 , y2),如果x1>x2 , 比较y1 , y2的大小.21. 某运输公司用10辆相同的汽车将一批苹果运到外地,每辆汽车能装8吨甲种苹果,或10吨乙种苹果,或11吨丙种苹果.公司规定每辆车只能装同一种苹果,而且必须满载.已知公司运送了甲、乙、丙三种苹果共100吨,且每种苹果不少于一车.(1)、设用x辆车装甲种苹果,y辆车装乙种苹果,求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若运送三种苹果所获利润的情况如下表所示:
设此次运输的利润为W(万元),问:如何安排车辆分配方案才能使运输利润W最大,并求出最大利润.