2018-2019学年初中数学华师大版八年级下册17.2.2 函数的图象 同步练习
试卷更新日期:2019-02-16 类型:同步测试
一、选择题
-
1. 甲、乙两人沿相同的路线从A到B匀速行驶,A,B两地间的路程为20 km,他们行进的路程s(km)与甲、乙出发的时间t(h)之间关系的图象如图所示,根据图象信息,下列说法正确的是( )
 A、甲的速度是4 km/h B、乙的速度是10 km/h C、乙比甲晚出发1 h D、甲比乙晚到B地3 h2. 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( )
A、甲的速度是4 km/h B、乙的速度是10 km/h C、乙比甲晚出发1 h D、甲比乙晚到B地3 h2. 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( ) A、喜羊羊与灰太狼最初的距离是30m B、灰太狼用15s追上了喜羊羊 C、灰太狼跑了60m追上了喜羊羊 D、灰太狼追上喜羊羊时,喜羊羊跑了60m3. 如图为某一天气温随时间的变化图,则下列说法不正确的是( )
A、喜羊羊与灰太狼最初的距离是30m B、灰太狼用15s追上了喜羊羊 C、灰太狼跑了60m追上了喜羊羊 D、灰太狼追上喜羊羊时,喜羊羊跑了60m3. 如图为某一天气温随时间的变化图,则下列说法不正确的是( ) A、这一天的最高气温为20 ℃ B、4时到12时,温度在上升 C、这一天的温差为10 ℃ D、这一天中,只有8点的温度为14 ℃4. 某市经常刮风,给人们出行带来很多不便,小明观测了某天连续 小时的风力情况,并绘出了风力随时间变化的图象,则下列说法中,正确的是( ).
A、这一天的最高气温为20 ℃ B、4时到12时,温度在上升 C、这一天的温差为10 ℃ D、这一天中,只有8点的温度为14 ℃4. 某市经常刮风,给人们出行带来很多不便,小明观测了某天连续 小时的风力情况,并绘出了风力随时间变化的图象,则下列说法中,正确的是( ). A、 时风力最小 B、
A、 时风力最小 B、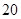 时风力最小
C、在 时至 时,风力最大为
时风力最小
C、在 时至 时,风力最大为 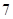 级
D、在 时至 14 时,风力不断增大
5. 放学后,小明倒了一杯开水,下列能近视刻画这杯水的水温y(℃)与时间t(h)的函数关系的图象是( )A、
级
D、在 时至 14 时,风力不断增大
5. 放学后,小明倒了一杯开水,下列能近视刻画这杯水的水温y(℃)与时间t(h)的函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、 6. 某人骑自行车沿直线旅行,先前进了a km, 又原路返回b km(b<a),休息了一段时间,再推车步行c km,此人离起点的距离y与时间x之间关系示意图象应为( )A、
6. 某人骑自行车沿直线旅行,先前进了a km, 又原路返回b km(b<a),休息了一段时间,再推车步行c km,此人离起点的距离y与时间x之间关系示意图象应为( )A、 B、
B、 C、
C、 D、
D、 7. 某地出租车计费方式如下:3 km以内只收起步价8元,超过3 km的除收起步价外,每超出1 km另加收2元;不足1 km的按1 km计费.则能反映该地出租车行驶路程x(km)与所收费用y(元)之间的函数关系的图象是( )A、
7. 某地出租车计费方式如下:3 km以内只收起步价8元,超过3 km的除收起步价外,每超出1 km另加收2元;不足1 km的按1 km计费.则能反映该地出租车行驶路程x(km)与所收费用y(元)之间的函数关系的图象是( )A、 B、
B、 C、
C、 D、
D、 8. 爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )A、
8. 爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )A、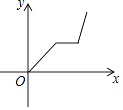 B、
B、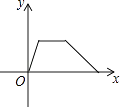 C、
C、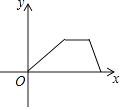 D、
D、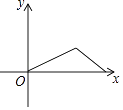 9. 一天,小芳去学校,她离开家不久,想起课本忘在家里,于是立即返回家里找到课本再去学校.下列四个图象中,能近似地刻画小芳这天上学过程的是( )A、
9. 一天,小芳去学校,她离开家不久,想起课本忘在家里,于是立即返回家里找到课本再去学校.下列四个图象中,能近似地刻画小芳这天上学过程的是( )A、 B、
B、 C、
C、 D、
D、 10.
10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、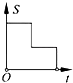 B、
B、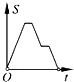 C、
C、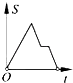 D、
D、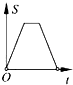
二、填空题
-
11.
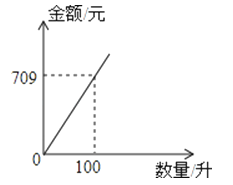
某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升 元.
 12.
12.河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有 米3的水,水泵最多抽 小时,水泵抽8小时后,河道剩水量是 米3 .
 13. 在全民健身环城越野赛中,甲、乙两名选手的行程y(千米)随时间x(时)变化的图象如图所示.有下列说法:①甲先到达终点;②起跑后1小时内,甲始终在乙的前面;③起跑1小时,甲、乙两人跑的路程相等;④乙起跑1.5小时,跑的路程为13千米;⑤两人都跑了20千米.以上说法正确的有(填序号).
13. 在全民健身环城越野赛中,甲、乙两名选手的行程y(千米)随时间x(时)变化的图象如图所示.有下列说法:①甲先到达终点;②起跑后1小时内,甲始终在乙的前面;③起跑1小时,甲、乙两人跑的路程相等;④乙起跑1.5小时,跑的路程为13千米;⑤两人都跑了20千米.以上说法正确的有(填序号). 14. 如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8点从同一地点出发,请你根据图中给出的信息,算出乌龟在点追上兔子.
14. 如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8点从同一地点出发,请你根据图中给出的信息,算出乌龟在点追上兔子. 15. 小明早晨从家骑车到学校,先上坡,后下坡,行驶情况如图所示,如果返回时上、下坡的速度与去学校时上、下坡的速度相同,那么小明从学校骑车回家用的时间是.
15. 小明早晨从家骑车到学校,先上坡,后下坡,行驶情况如图所示,如果返回时上、下坡的速度与去学校时上、下坡的速度相同,那么小明从学校骑车回家用的时间是. 16. 如图是甲、乙两名运动员在自行车比赛中所走路程与时间的关系图象,则甲的速度乙的速度(用“>”“=”或“<”填空).
16. 如图是甲、乙两名运动员在自行车比赛中所走路程与时间的关系图象,则甲的速度乙的速度(用“>”“=”或“<”填空). 17.
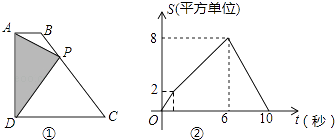
17.如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 .
三、解答题
-
18. 温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
 (1)、这一天的最高温度是多少?是在几时到达的?最低温度呢?(2)、这一天的温差是多少?从最低温度到最高温度经过多长时间?(3)、在什么时间范围内温度在上升?在什么时间范围内温度在下降?19. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)、这一天的最高温度是多少?是在几时到达的?最低温度呢?(2)、这一天的温差是多少?从最低温度到最高温度经过多长时间?(3)、在什么时间范围内温度在上升?在什么时间范围内温度在下降?19. 小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示). (1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、10时和13时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、11时到12时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?20. 某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答问题.
(1)、图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)、10时和13时,他分别离家多远?(3)、他到达离家最远的地方是什么时间?离家多远?(4)、11时到12时他行驶了多少千米?(5)、他可能在哪段时间内休息,并吃午餐?(6)、他由离家最远的地方返回时的平均速度是多少?20. 某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答问题. (1)、机动车行驶几小时后加油?(2)、中途加油L;(3)、如果加油站距目的地还有240km,车速为40km/h,要到达目的地,油箱中的油是否够用?并说明原因.21. 已知y与x的关系的图象如图所示,根据图象回答下列问题:
(1)、机动车行驶几小时后加油?(2)、中途加油L;(3)、如果加油站距目的地还有240km,车速为40km/h,要到达目的地,油箱中的油是否够用?并说明原因.21. 已知y与x的关系的图象如图所示,根据图象回答下列问题: (1)、确定自变量x的取值范围.(2)、当x=-4,-2,4时,y的值分别是多少?(3)、当y=0,4时,x的值分别是多少?(4)、当x取何值时,y的值最大?当x取何值时,y的值最小?(5)、当x的值在什么范围内时,y随x的增大而增大?当x的值在什么范围内时,y随x的增大而减小?22. 下面是一位病人的体温记录图,看图回答下列问题:
(1)、确定自变量x的取值范围.(2)、当x=-4,-2,4时,y的值分别是多少?(3)、当y=0,4时,x的值分别是多少?(4)、当x取何值时,y的值最大?当x取何值时,y的值最小?(5)、当x的值在什么范围内时,y随x的增大而增大?当x的值在什么范围内时,y随x的增大而减小?22. 下面是一位病人的体温记录图,看图回答下列问题: (1)、护士每隔几小时给病人量一次体温?(2)、这位病人的最高体温是多少摄氏度?最低体温是多少摄氏度?(3)、他在4月8日12时的体温是多少摄氏度?(4)、图中的横线表示什么?(5)、从图中看,这位病人的病情是恶化还是好转?23. 甲、乙两人共同加工一批零件,从工作开始到加工完这批零件,两人恰好同时工作6小时,两人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题:
(1)、护士每隔几小时给病人量一次体温?(2)、这位病人的最高体温是多少摄氏度?最低体温是多少摄氏度?(3)、他在4月8日12时的体温是多少摄氏度?(4)、图中的横线表示什么?(5)、从图中看,这位病人的病情是恶化还是好转?23. 甲、乙两人共同加工一批零件,从工作开始到加工完这批零件,两人恰好同时工作6小时,两人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图象如图所示,根据信息回答下列问题: (1)、请解释图中点C的实际意义;(2)、求出甲、乙在整个过程中的函数表达式(并注明自变量的范围);(3)、如果甲、乙两人完成同样数量的零件时,甲比乙少用1小时,那么此时甲、乙两人各自完成多少个零件?
(1)、请解释图中点C的实际意义;(2)、求出甲、乙在整个过程中的函数表达式(并注明自变量的范围);(3)、如果甲、乙两人完成同样数量的零件时,甲比乙少用1小时,那么此时甲、乙两人各自完成多少个零件?