浙江省重点中学2018-2019学年高三数学12月期末热身联考试卷
试卷更新日期:2019-02-12 类型:高考模拟
一、单选题
-
1. 已知M={x|x>1},N={x|x2-2x-8≤0},则 =( )A、[-4,2) B、(1,4] C、(1,+∞) D、(4,+∞)2. 已知i为虚数单位,复数 ,则 =( )A、1 B、2 C、 D、53. 已知双曲 的一条渐近线方程为 ,则该双曲线的离心率是( )A、
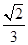 B、
C、2
D、
B、
C、2
D、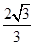 4. 已知 ,则“m⊥n”是“m⊥l”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 函数 的大致图像是( )A、
4. 已知 ,则“m⊥n”是“m⊥l”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 函数 的大致图像是( )A、 B、
B、 C、
C、 D、
D、 6. 展开式中, 的系数是( )A、80 B、-80 C、40 D、-407. 已知实数x,y满足约束条件 ,则z=x+4y的取值范围是( )A、[-6,4] B、[2,4] C、[2,+∞) D、[4,+∞)8. 已知函数 ,若 恒成立,则实数a的最小正值为( )A、2
6. 展开式中, 的系数是( )A、80 B、-80 C、40 D、-407. 已知实数x,y满足约束条件 ,则z=x+4y的取值范围是( )A、[-6,4] B、[2,4] C、[2,+∞) D、[4,+∞)8. 已知函数 ,若 恒成立,则实数a的最小正值为( )A、2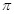 B、
B、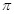 C、
C、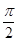 D、
D、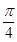 9. 已知方程 有且仅有两个不同的实数解 ,则以下有关两根关系的结论正确的是( )A、
9. 已知方程 有且仅有两个不同的实数解 ,则以下有关两根关系的结论正确的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,将边长为2的正方形ABCD沿PD、PC翻折至A、B两点重合,其中P是AB中点,在折成的三棱锥A(B)-PDC中,点Q在平面PDC内运动,且直线AQ与棱AP所成角为60º,则点Q运动的轨迹是( )
10. 如图,将边长为2的正方形ABCD沿PD、PC翻折至A、B两点重合,其中P是AB中点,在折成的三棱锥A(B)-PDC中,点Q在平面PDC内运动,且直线AQ与棱AP所成角为60º,则点Q运动的轨迹是( ) A、圆 B、椭圆 C、双曲线 D、抛物线
A、圆 B、椭圆 C、双曲线 D、抛物线二、填空题
-
11. 已知随机变量的 的分布列为:

若E( )= ,则x+y=;D( )=
12. 若 =6,则 =; =13. 某空间几何体的三视图如图所示,则该几何体的体积是;表面积是 14. 已知直线 .若直线 与直线 平行,则 的值为;动直线 被圆 截得弦长的最小值为 .15. 向量 , 满足:| |=2,| + |=1,则 的最大值为
14. 已知直线 .若直线 与直线 平行,则 的值为;动直线 被圆 截得弦长的最小值为 .15. 向量 , 满足:| |=2,| + |=1,则 的最大值为
16. 如图,有7个白色正方形方块排成一列,现将其中4块涂上黑色,规定从左往右数,无论数到第几块,黑色方块总不少于白色方块的涂法有种。 17. 平行六面体ABCD-A1B1C1D1中,已知底面四边形ABCD为矩形,∠A1AB=∠A1AD= 。其中|AB|=a,|AD|=b,|AA1|=c,体对角线|A1C|=1,则c的最大值为
17. 平行六面体ABCD-A1B1C1D1中,已知底面四边形ABCD为矩形,∠A1AB=∠A1AD= 。其中|AB|=a,|AD|=b,|AA1|=c,体对角线|A1C|=1,则c的最大值为三、解答题
-
18. 已知a,b,c分别为△ABC三个内角A,B,C的对边,且满足: 。(1)、求∠A。(2)、若D是BC中点,AD=3,求△ABC的面积。19. 如图,等腰直角三角形ABC中,∠B是直角,平面ABEF⊥平面ABC,2AF=AB=BE,∠FAB=60º,AF∥BE。
 (1)、求证:BC⊥BF;(2)、求直线BF与平面CEF所成角的正弦值。
(1)、求证:BC⊥BF;(2)、求直线BF与平面CEF所成角的正弦值。
