浙江省温州市“十五校联合体”2018-2019学年高一上学期数学期中联考试卷
试卷更新日期:2019-02-12 类型:期中考试
一、单选题
-
1. 已知集合P={-1,0,1,2},Q={-1,0,1},则( )A、
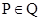 B、
B、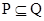 C、
C、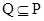 D、
D、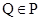 2. 已知幂函数f(x)=xa过点(4,2),则f(x)的解析式是( )A、
2. 已知幂函数f(x)=xa过点(4,2),则f(x)的解析式是( )A、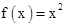 B、
B、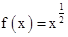 C、
C、 D、
D、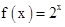 3. 设f(x)= ,则下列结论错误的是( )A、
3. 设f(x)= ,则下列结论错误的是( )A、 B、
B、 C、
C、 D、
D、 4. 函数f(x)=x2-2x+t(t为常数,且t∈R)在[-2,3]上的最大值是( )A、
4. 函数f(x)=x2-2x+t(t为常数,且t∈R)在[-2,3]上的最大值是( )A、 B、
B、 C、
C、 D、
D、 5. 已知函数 ,则 ( )A、是奇函数,且在R上是增函数 B、是偶函数,且在R上是增函数 C、是奇函数,且在R上是减函数 D、是偶函数,且在R上是减函数6. 已知集合 ,则 ( )A、
5. 已知函数 ,则 ( )A、是奇函数,且在R上是增函数 B、是偶函数,且在R上是增函数 C、是奇函数,且在R上是减函数 D、是偶函数,且在R上是减函数6. 已知集合 ,则 ( )A、 B、
B、 C、
C、 D、
D、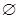 7. 已知函数 (其中 )的图象如右图所示,则函数 的图象是( )
7. 已知函数 (其中 )的图象如右图所示,则函数 的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 给出下列三个等式:f(x+y)=f(x)•f(y),f(x•y)=f(x)+f(y),f(ax+by)=af(x)+bf(y)(a+b=1).下列选项中,不满足其中任何一个等式的是( )A、
8. 给出下列三个等式:f(x+y)=f(x)•f(y),f(x•y)=f(x)+f(y),f(ax+by)=af(x)+bf(y)(a+b=1).下列选项中,不满足其中任何一个等式的是( )A、 B、
B、 C、
C、 D、
D、 9. 函数 的值域是( )A、
9. 函数 的值域是( )A、 B、
B、 C、
C、 D、
D、 10. 函数 的所有零点的积为m,则有( )A、
10. 函数 的所有零点的积为m,则有( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知集合A={1,2},集合B满足A∪B={1,2,3},则集合A的子集个数有个;这样的集合B有个.12. 函数y=ln(x-1)的定义域为;函数y=ln(x-1)的值域为 .13. 已知函数 ,则f(f(-1))=;不等式f(x)≥1的解集为 .14. lg4+2lg5=;若loga2=m,loga3=n,则 = .15. 若2x+1<22-x , 则实数x的取值范围是 .16. 设函数 ,函数 ,则f(-x)g(-x)+f(x)g(x)=17. 已知函数 ,关于x的方程f(x)=a有2个不同的实根,则实数a的取值范围为 .
三、解答题
-
18. 已知集合A={x|0<x+2≤7},集合B={x|x2-4x-12≤0},全集U=R,求:
(Ⅰ)A∩B;
(Ⅱ)A∩(∁UB).
19. 计算:(Ⅰ) ;
(Ⅱ)设3x=4y=6,求 的值.