浙江省湖州市八校联盟2018-2019学年高一上学期数学期中联考试卷
试卷更新日期:2019-02-12 类型:期中考试
一、单选题
-
1. 设全集U={1,2,3},集合A={1,2},则∁UA等于( )A、
 B、
B、 C、
C、 D、
D、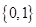 2. 下列函数中,定义域是R且为增函数的是( )A、
2. 下列函数中,定义域是R且为增函数的是( )A、 B、
B、 C、
C、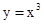 D、
D、 3. 若幂函数y=f(x)的图象经过点(3, ),则f(2)=( )A、2 B、
3. 若幂函数y=f(x)的图象经过点(3, ),则f(2)=( )A、2 B、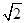 C、
D、4
4. 函数 的零点在区间( ).A、
C、
D、4
4. 函数 的零点在区间( ).A、 B、
B、 C、
C、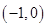 D、
D、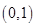 5. 设f:x→ln|x|是集合M到集合N的映射,若N={0,1},则M不可能是( )A、
5. 设f:x→ln|x|是集合M到集合N的映射,若N={0,1},则M不可能是( )A、 B、
B、 1,
1,  C、
C、 D、
D、 1,
1,  6. 下列等式一定正确的是( )A、
6. 下列等式一定正确的是( )A、 B、
B、 C、
C、 D、
D、 7. 设a=ln2,b=(lg2)2 , c=lg(lg2),则( )A、
7. 设a=ln2,b=(lg2)2 , c=lg(lg2),则( )A、 B、
B、 C、
C、 D、
D、 8. 若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x-1)<0的解集是( )A、(-1,0) B、(-∞,0)∪(1,2) C、(1,2) D、(0,2)9. 已知1是函数f(x)=ax2+bx+c(a>b>c)的一个零点,若存在实数x0 . 使得f(x0)<0.则f(x)的另一个零点可能是( )A、
8. 若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x-1)<0的解集是( )A、(-1,0) B、(-∞,0)∪(1,2) C、(1,2) D、(0,2)9. 已知1是函数f(x)=ax2+bx+c(a>b>c)的一个零点,若存在实数x0 . 使得f(x0)<0.则f(x)的另一个零点可能是( )A、 B、
B、 C、
C、 D、
D、 10. 已知二次函数f(x)=x2+bx+c,若对任意的x1 , x2∈[-1,1],有|f(x1)-f(x2)|≤6,则b的取值范围是( )A、
10. 已知二次函数f(x)=x2+bx+c,若对任意的x1 , x2∈[-1,1],有|f(x1)-f(x2)|≤6,则b的取值范围是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 已知log23=a,则log29=(用a表示),2a= .12. 计算 ;函数 值域是13. 已知函数f(x),g(x),分别由下表给出
x
1
2
3
f(x)
2
1
1
x
1
2
3
g(x)
3
2
1
则g(1)的值为;当g[f(x)]=2时,x= .
14. 已知f(x)=ax2+(b-1)x+2a是定义域为[a-1,a]的偶函数,则a-b的值为;函数g(x)=loga(-bx2+a)的单调递增区间为15. 设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+m,则f(﹣1)= .16. 设2a=5b=m,且 =2,则m= .17. 若函数f(x)=(1-x2)(x2+bx+c)的图象关于直线x=-2对称,则b+c的值是 .三、解答题
-
18. 已知集合A={x|m-2<x<m+1},B={x|1<x<5}.
(Ⅰ)若m=1,求A∪B;
(Ⅱ)若A∩B=A,求实数m的取值范围.
19. 已知函数f(x)= +lg(3x )的定义域为M.(Ⅰ)求M;
(Ⅱ)当x∈M时,求g(x)=4x-2x+1+2的值域.
20. 已知函数f(x)= (k∈R)(Ⅰ)若该函数是偶函数,求实数k及f(log32)的值;
(Ⅱ)若函数g(x)=x+log3f(x)有零点,求k的取值范围.